作為一個合格的 DBA,在遇到線上單表數據量超過千萬級別的時候,往往會建議使用者透過分表來縮減單表數據量,當使用者問為什麽單表數據量不能超過千萬時,DBA 往往會說:單表數據量超過千萬,會影響查詢效能。
知其然而不知所以然,學習技術不能停留在表面,而是要進一步去深入挖掘其中的原理,這樣才能不斷進步和成長。回到這個問題:為什麽單表數據量不能超過兩千萬,其中的依據是什麽?
事情是這樣的:
小王最近參加了騰訊的技術面試,面試官向他提了一個經典的面試問題:聊聊你日常計畫裏的分庫分表實踐?
於是小王以過往計畫裏的某個 case 為例做了回答:
我負責的計畫裏涉及到儲存使用者操作記錄的功能,因為每天的數據量比較大,差不多超過 5000 萬條,所以我另外又做了分庫分表的操作。系統會自動定時生成 3 張表,數據分別儲存其中,防止都放在一個表裏面導致查詢效能降低。
面試官又問:這裏為什麽要做一個分庫分表的操作呢?如果放在同一張表裏面,為什麽會導致查詢效能降低?
小王內心 OS:為什麽1+1=2?但他還是語氣平常地回答說:
MySQL 單表不要超過 2000 萬行基本上是一個行業共識,只有當單表行數超過 500 萬行或者單表容量超過 2GB,我們一般才推薦進行分庫分表。
面試官點了點頭表示認可,卻也沒有在這個問題上繼續深究,繼而問起了別的問題,不久後就結束了面試。小王回過神來以後復盤這次面試過程,覺得自己在 MySQL 分庫分表問題上沒有回答得特別到位,於是他開始進一步地深究起來這個「1+1=2」的問題。
一、自增主鍵角度
我們先來看看單表數據量理論上最大值是多少?
假設我們建表,ID 是自增主鍵,也就是說主鍵的大小可以限制表的上限。如果主鍵聲明為 int 型別,那麽 int 型別最大為2的32次方 – 1 ,也就是21億左右;
如果主鍵聲明為 bigint 型別,那麽 bigint 型別最大為2的64次方 – 1,這個數位實在太大了,一般還沒到這個限制,磁盤就撐不住了;
如果主鍵聲明為tinyint型別,那麽 tinyint 型別最大為2的8次方 – 1,也就是255,所以如果我插入一條 ID=256 的數據,就會報錯;
上面是從自增主鍵的角度來講述單表最大數據量理論上能達到多少,那麽接下來從另一個角度「數據頁」來闡述一下,單表數據量最大能達到多少,依據是什麽?
二、數據頁角度
假設我們有一張 user 表,其中 ID 是自增主鍵,那麽該表在硬碟檔上是 user.ibd(innodb 數據檔,又叫表空間檔)。這個數據檔被劃分成很多的數據頁,每個數據頁大小是16K。
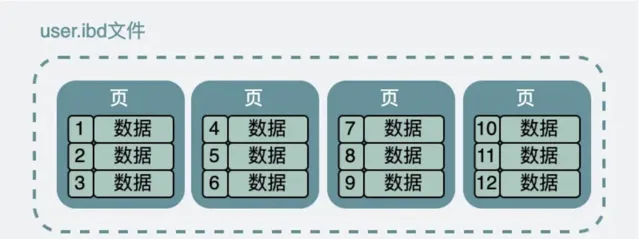
一個數據頁16K,表的數據量很多,一個數據頁可能放不下那麽多數據,所以數據被分成好多份,存放在不同的數據頁,為了標識具體是哪一個數據頁,所以需要有頁號來標識;
同時為了把這些存放數據的數據頁關聯起來,又引入了前後指標,用於指向前後的頁;
數據頁需要讀寫,寫入到一半的過程中可能會發生了意外斷電等情況,所以為了保證數據頁的準確性,還引入了校驗碼;
同時為了在數據頁搜尋數據提高效率,數據頁內部還生成了頁目錄;
除了上述所說的,數據頁內剩下的空間就用來存放實際的數據;
即數據頁的結構如下:
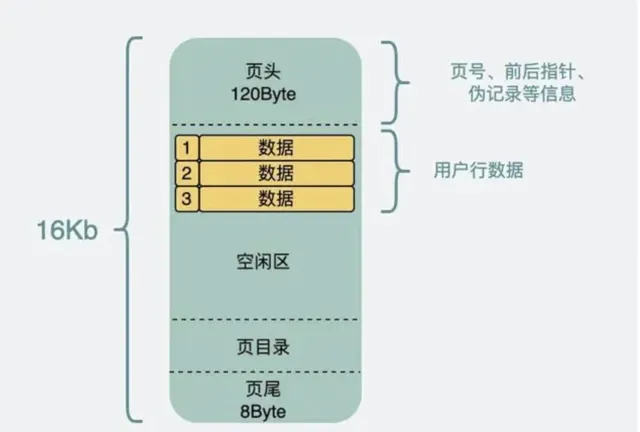
數據是以數據頁的形式進行儲存,數據頁和數據頁之間是以B+樹的形式進行關聯,例如:
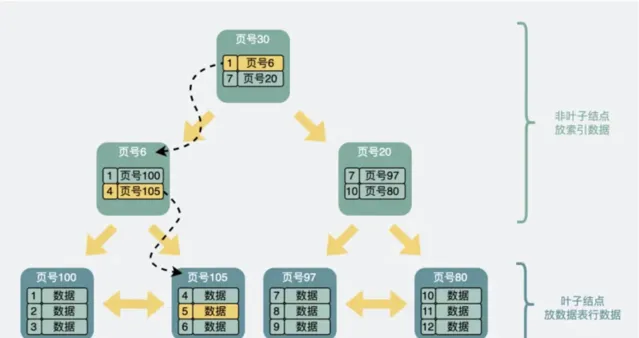
其中,葉子節點的數據頁存放的是實際儲存的數據,非葉子節點存放的是索引內容。B+樹的每一層代表一次磁盤 IO。
舉個例子,如果我要尋找 ID=5 的記錄,從頂部非葉子節點開始尋找,由於 ID=5 大於1並且小於7,故應該往左邊尋找,來到頁號為6的數據頁,由於5大於4,故應該往右邊尋找,來到頁號為105的數據頁,找到 ID=5 的記錄,完成查詢。
這個過程中查詢了三個數據頁,如果這三個數據頁都沒有載入到記憶體,那麽就需要經歷三次磁盤 IO 查詢。
了解完 B+樹是如何儲存數據的,我們就可以開始進行數據的估算。
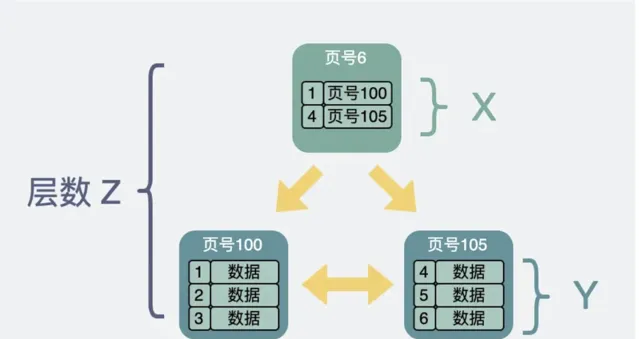
假設:非葉子節點內指向其他數據頁的指標數量為 X(即非葉子節點的最大子節點數為 X);每個葉子節點可以儲存的行記錄數為 Y;B+樹的高度為 N(即 B+樹的層數);
對於一個高度為 N 的 B+樹,頂層(根節點)有一個非葉子節點,那麽第二層就有X個節點,第三層就有 X 的2次方個節點,第四層就有 X 的三次方個節點,以此類推,第 N 層(即葉子節點所在的第 N 層)就有 X 的 N-1 次方個節點;
在 B+ 樹中,所有的記錄都儲存在葉子節點中,假設每個葉子節點都可以儲存的行記錄數為 Y;
那麽 B+ 樹可以儲存的數據總量為葉子節點總數乘以每個葉子節點儲存的記錄數,即:M=(X 的 N-1 次方)乘以 Y;
代入計算:
一個數據頁大小16K,扣除頁號、前後指標、頁目錄,校驗碼等資訊,實際可以儲存數據的大約為15K,假設主鍵ID為bigint型,那麽主鍵 ID 占用8個 byte,頁號占用4個 byte,則 X=15*1024/(8 + 4) 等於1280;
一個數據頁實際可以儲存數據的空間大小,大約為15K,假設一條行記錄占用的空間大小為1K,那麽一個數據頁就可以儲存15條行記錄,即 Y=15;
假設 B+樹是兩層的:則 N=2,即 M=1280的(2-1)次方 * 15 ≈ 2w ;
假設 B+樹是三層的:則 N=3,即 M=1280的2次方 * 15 ≈ 2.5 kw;
假設 B+樹是四層的:則 N=4,即 M=1280的3次方 * 15 ≈ 300億 ;
綜上所述,我們建議單表數據量大小在兩千萬。當然這個數據是根據每條行記錄的大小為 1K 的時候估算而來的,而實際情況中可能並不是這個值,所以這個建議值兩千萬只是一個建議,而非一個標準。
三、思考
最後考一個問題:一個4層的 B+樹,主鍵是 bigint 型,一條記錄平均長度是1K,不考慮碎片,能存放多少條記錄?
答案:
根據 B+樹儲存數據的計算公式:M = X 的 N-1 次方 * Y:
一個數據頁大小16K,扣除頁號、前後指標、頁目錄,校驗碼等資訊,實際可以儲存數據的大約為15K,假設主鍵 ID 為 bigint 型,那麽主鍵 ID 占用8個 byte,頁號占用4個byte,則X=15*1024/(8 + 4) 等於1280;
每條記錄1K大小,一個數據頁有15K是用來儲存數據的,那麽一個數據頁就能儲存15條記錄;
所有葉子節點數量為 X 的 N-1 次方,即1280*1280*1280;儲存的記錄數總數為:葉子節點數量 * 每個葉子節點儲存的記錄數,所以 M = 1280*1280*1280*15。
你,學會了嗎?
作者丨肖浩騰
來源丨公眾號:騰訊雲開發者(ID:QcloudCommunity)
dbaplus社群歡迎廣大技術人員投稿,投稿信箱: [email protected]












