2024-02-24碼農

AI代面來了，真的太牛逼了，這錢賺的，嘎嘎多！！！

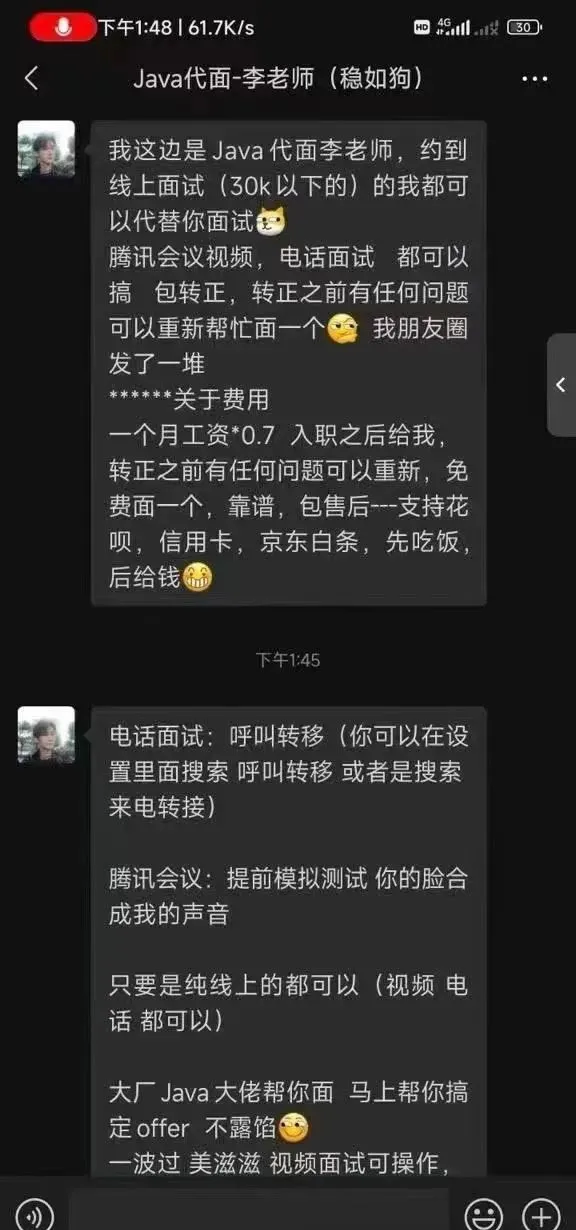
看明白了把，所謂的AI代面其實就是，即時換臉聲音替換。

想一想，技術大佬用AI技術把自己變成你的模樣，還能模仿你的聲音，然後去幫你面試，比獵頭的服務更全面！

這事兒，真的是挺逗的。想想看，如果有一天，大廠面試全變成了AI代面的戰場，那面試官和面試者之間的遊戲，就變成了一場「誰的AI更厲害」的較量。

不過，話說回來，這種方式雖然聽起來能讓人輕松入職大廠，但總感覺像是在玩一場沒有硝煙的戰爭。畢竟，工作不僅僅是面試，面試過了，工作上的事還得自己來。

所以，AI代面這玩意兒，雖然能讓人一時爽，但最終還是得靠自己的實力說話。

不過，就這技術本身而言，不得不說，確實挺有創意，也挺好玩的。

下面是今天的演算法題

# 最長回文子串

演算法題目

給定一個字串 s，找到 s 中最長的回文子串。

引言

在字串處理的眾多問題中，尋找最長回文子串是一個既經典又具有挑戰性的問題。它不僅考驗著程式設計師對字串操作的熟練程度，還涉及到了對演算法最佳化的理解。本文將透過中心擴充套件演算法詳細介紹如何尋找一個字串中的最長回文子串，同時提供C語言、Java和Python的實作程式碼。

演算法思路

中心擴充套件演算法的核心思想是：對字串中的每一個字元，嘗試以該字元為中心向兩邊擴充套件，尋找最長的回文串。由於回文串的中心可能是一個字元（如"aba"），也可能是兩個字元（如"abba"），因此需要對字串中的每個字元進行兩次中心擴充套件。

具體步驟如下：

初始化最長回文子串的起始位置和最大長度。
遍歷字串中的每個字元，對於每個字元，執行兩次中心擴充套件：

以該字元為中心的奇數長度回文。

以該字元和下一個字元為中心的偶數長度回文。

比較並更新最長回文子串的資訊。

返回最長回文子串。

程式碼實作

C語言實作

#include<stdio.h>#include<string.h>voidexpandAroundCenter(constchar *s, int left, int right, int *start, int *maxLen){while (left >= 0 && right < strlen(s) && s[left] == s[right]) { left--; right++; }if (*maxLen < right - left - 1) { *start = left + 1; *maxLen = right - left - 1; }}char* longestPalindrome(char* s){int start = 0, maxLen = 0;for (int i = 0; i < strlen(s); i++) { expandAroundCenter(s, i, i, &start, &maxLen); // 奇數長度 expandAroundCenter(s, i, i + 1, &start, &maxLen); // 偶數長度 }char *result = (char*)malloc(sizeof(char) * (maxLen + 1));strncpy(result, s + start, maxLen); result[maxLen] = '\0';return result;}

Java實作

public classSolution {public String longestPalindrome(String s) {if (s == null || s.length() < 1) return"";int start = 0, end = 0;for (int i = 0; i < s.length(); i++) {int len1 = expandAroundCenter(s, i, i); // 奇數長度int len2 = expandAroundCenter(s, i, i + 1); // 偶數長度int len = Math.max(len1, len2);if (len > end - start) { start = i - (len - 1) / 2; end = i + len / 2; } }return s.substring(start, end + 1); }privateintexpandAroundCenter(String s, int left, int right) {while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) { left--; right++; }return right - left - 1; }}

Python實作

def longest_palindrome(s: str) -> str: def expand_around_center(left: int, right: int) -> str:whileleft >= 0 and right < len(s) and s[left] == s[right]:left -= 1right += 1return s[left + 1:right]if not s:return"" start, end = 0, 0for i in range(len(s)): len1 = len(expand_around_center(i, i)) len2 = len(expand_around_center(i, i + 1)) max_len = max(len1, len2)if max_len > end - start: start = i - (max_len - 1) // 2 end = i + max_len // 2return s[start:end + 1]