强力推荐：算法学习从放弃到入门的第一步，我花了 42 天终于走完了

你是不是像我一样，是一名算法学习困难户，每一次都满怀希望地开始，却又每一次失望地结束。

如果这听起来很熟悉，那么这篇文章正是为你而写。我们将以全新的视角来探究算法，采用一种更符合我们大脑自然思维方式的学习方法。

我们将追溯排序算法的源头，探讨它们在当代编程应用中的演变。每一个环节都充满挑战和启发。

让我们追随那些伟大的算法先驱，揭开数据排序的秘密，理解它们的本质，尝试真正地走入一次算法学习的大门。

01

算法学习的困惑

打开任何一本算法相关的书籍，我们常常看到它们从排序算法讲起。我一直有这么一个困惑，不知道你有没有，就是为什么要学习排序算法？

对于程序员而言，排序是一个简单的任务，比如 SQL 中使用「ORDER BY」，或者代码中使用「sort()」方法，就可以快速完成排序。

更让人觉得可气的是，认真学习一段时间后，我们发现书上学来的排序算法，性能完全比不上这些简单的调用。

这会让人很有挫败感，因为算法学习逐渐从实用驱动，变成了面试驱动，它成为了检测你学习和理解能力的工具。

此外，算法的固有复杂性确实使得其学习成为一项挑战。当学习变得抽象且缺乏直接的应用价值时，大多数人的学习方法也变成了死记硬背，学完就忘。

一不小心，学习算法就像学习英语一样，一次次地翻开书本，一次次地背到「abandon」后就无疾而终了。

有没有一种可能，学不好算法的原因不是因为我们自己，而是教科书的教学方式本身就是错的？

02

学习算法就是学习历史

为什么简单调用一个排序方法，其性能会超过许多教科书上的算法呢？

答案其实很简单：这些书中的算法大多源于上世纪五六十年代，而你所调用的，则是经过无数工程师优化之后的现代算法。

计算机发展的时间太短了，让人很容易忽略它也是有历史的。

以数学为例，我们可以更容易理解这一点。古希腊哲学家芝诺对无穷悖论的探索，与牛顿和莱布尼茨对无穷问题的处理，显然是不一样的。

你也许没听说过芝诺这个名字，因为在微积分的教科书中很少提及。然而，在介绍微积分发展历程的书籍里，他是绝对不能缺席的。

从问题到答案的过程中，人类对无穷问题的理解是渐进式的。但教科书往往只给我们最终的答案和方法，忽略了其中的思维过程。

算法书籍也存在这样的问题。书中对每个算法的介绍都很详尽，但它们略过了这些算法的发展历史，其诞生和演变的过程，以及可能走过的弯路。

这非常不符合人类大脑学习和记忆的过程。如果我们将这一环节补上，将算法学习视为一次历史之旅，会怎样呢？

重走一遍从无到有的发现历程，深入理解其中的思考过程，不仅有助于我们掌握算法的逻辑本质，也有利于理解计算机思维。

03

数据大爆发

在计算机时代到来之前，你有没有想过数据是如何被排序的？

在古代，县衙的书记员会手动将公文、税收等文件进行分类归档，通常依据类别和日期排序，以便于将来的检索。

但是，当数据量增长到超出人力可处理的范围时，应该如何应对呢？

19 世纪末，随着美国人口的快速增长，人口普查的数据处理成为了一项巨大的挑战。

从 1870 年的 5 个调查科目增加到 1880 年的 200 多个，仅完成 1880 年人口普查的工作就耗时长达 8 年，数据量的大爆炸成为了当时急需解决的问题。

当时，数据被记录在打孔卡片上，每张卡片上的孔洞代表了不同的信息。

面对成堆的打孔卡片，如何有效进行排序成为了一个问题，比如如何根据年龄对卡片进行排序。

IBM 提供了一种解决方案，即 IBM Sorter 机器，专门用于对打孔卡片进行排序。

IBM Sorter 的工作原理，实际上是基数排序（Radix Sort）的一个物理实现。

机器拥有 13 个口袋，其中 12 个用于分类卡片上对应的十二行的信息，还有一个口袋用于处理空白、拒绝和错误的卡片。

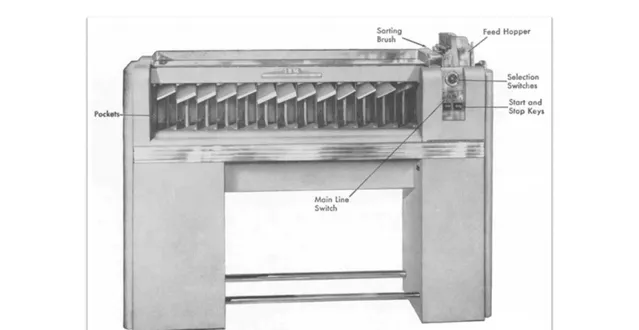
在排序开始前，操作员需要设置好机器，以确定哪一列数据将被用于排序。

例如，如果我们首先根据年龄的个位数排序，机器便会按照这一标准运行，卡片将根据年龄的个位数被分配到不同的口袋中。

随后，通过对这些个位数已经排序的卡片进行进一步的排序——这次是依据年龄的十位数，我们可以完成全面的排序工作。

进一步地，IBM 还开发了 IBM Collator，这是一种能够实现两堆已排序卡片合并的机器。

它的工作原理类似于合并排序算法，即将两组已经排序的数据合并成一组有序的数据集。

这些机械式的排序方法，效率远远高于当时的人力，它们向我们展示了利用机械化手段处理大规模数据的可能性。

在计算机发明之前，我们已经能够见证基数排序（Radix Sort）和合并排序在现实世界中的应用。

这不仅是对技术创新的一种展示，也反映了算法和数据处理技术的发展是一个长期而渐进的过程。

04

拯救计算机的算力

在20世纪40年代，计算机的诞生开启了数字处理的新时代。

早期的计算机通过数字逻辑电路执行计算任务，如求解微分方程以计算弹道路径，显示了计算机在处理复杂计算方面的巨大潜力。

计算机设计中的逻辑和数学问题引起了冯·诺依曼的兴趣。

作为研发小组的顾问，他试图解决早期计算机设计中的缺陷，并最终提出了存储程序计算机概念，即著名的冯·诺依曼架构。这一架构为现代计算机的设计奠定了基础。

为验证这种设计的实用性，冯·诺依曼选择排序作为主题，通过比较计算机执行这些算法的时间与 IBM Collator 这类专用排序机的处理速度来展示计算机的效率。

这也是冯·诺依曼写的第一个程序，当年是写在手稿上，高德纳发现后将其改写为符号化的汇编语言。

人们逐渐发现计算机不仅能完成简单的数据合并任务，还能实现更复杂的完整排序过程。

数据不再存储在卡片上，而是直接保存在连续的内存中，可以通过指针移动来进行排序，从而产生了诸如冒泡排序、选择排序和插入排序等简单的排序算法。

这些基本的排序方法，它们像打麻将时整理牌一样，在内存中重新排列数据。

？

随着计算机的普及，研究人员发现，大量的计算机算力被用于执行排序操作，估计高达 30% 的算力用于此目的。

这促使了排序算法进入内卷的时代。

为了优化算力的使用，开发者开始探索新的算法，比如使用递归和分治编程技巧的归并排序。

？

归并排序算法虽然有效，但也暴露出对内存空间的高需求。

1959年，英国科学家 Tony Hoare 提出了快速排序算法，它基于相同的递归和分治思想，但在内存使用上更为高效。

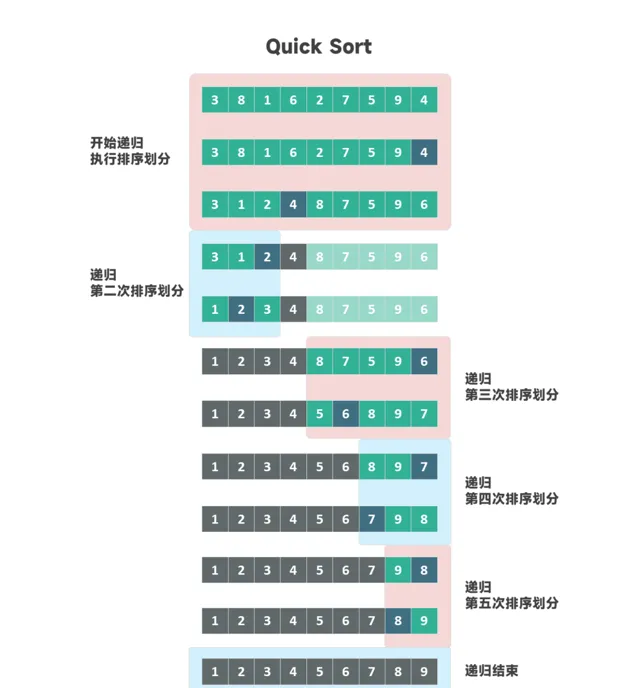
尽管快速排序解决了内存使用问题，但它无法保证排序的稳定性——即无法保证相同元素的原始顺序。

1964 年加拿大科学家 J.W.J. Williams 发明的堆排序，这种算法利用堆这一数据结构，提供了又一种排序的解决方案。

这些算法各有优缺点，哪种算法更好？评判标准又是什么？

05

建立评判标准

面对不同场景下算法性能的评价问题，计算机科学界长期缺乏一个统一的评价标准。

这一问题引发了广泛的讨论，直到 1965 年，Juris Hartmanis 和 Richard Stearns 提出算法复杂度的概念，为这一讨论提供了新的方向。

最终，高德纳通过引入 Big O 表示法，提出了一种量化衡量算法复杂度的方法，他也因此被称为「算法分析之父」。

高德纳提出的算法复杂度分析有两个核心原则：

1. 在评估算法效率时，应考虑处理极大数据量的场景。之所以关注极大数据量，是因为计算机的设计初衷就是为了处理日益增长的数据量。

2. 虽然影响算法性能的因素众多，但它们可大致分为两类：一类是与数据量无关的固定因素，另一类则是随数据量增长而变化的因素。在评价算法优劣时，关键在于考察在处理接近无限大的数据集时算法的表现。

通过这种方法，我们能够将排序算法分为两大类：

时间复杂度为 O(n²) 的算法，如冒泡排序、选择排序、插入排序。

时间复杂度为 O(nlog(n)) 的算法，如归并排序、快速排序、堆排序。

这一划分不仅帮助了研究者和开发者在选择算法时做出更合理的决策，也促进了计算机科学领域对算法性能评价标准的统一，推动了计算机算法的进一步优化和发展。

06

回归排序的本质

在探讨排序算法的发展时，一定会遇到这个问题：是否达到 O(nlog(n)) 的排序算法就是最优？

要回答这个问题，我们需要从头开始，重新审视排序的本质。

排序的核心是确定一组元素间的相对顺序。对于任意 N 个元素，存在 N! （N 的阶乘）种可能的排列，我们的任务是从中找到那唯一满足排序条件的排列。

排序问题可以被认为是确定元素之间的相对顺序。对于任何给定的 N 个元素，都有 N! （N的阶乘）种可能的排列，我们的目标是找出那唯一的一种满足排序需求的排列。

通过比较元素的方式，我们尝试找到这个「最小」的排列。每次比较实质上是一个二选一的决策，就像猜数字游戏中的问题，只有「是」或「否」两种可能。

理想情况下，每次比较都应该将可能性空间平均分割为两半，这是二分法最优解的基础，也是比较排序的本质。

从排序算法的本质出发，我们得出结论：比较排序的理论上限是 O(nlogn) 。

究竟哪种排序算法最接近这一理论上限呢？答案是那些每次比较都能尽可能将结果分为两等份的算法。

通过比较我们可以看到优化过的快速堆排序更接近理论上限。

这种对排序本质的探索不仅涵盖了二分法与排序效率的关系，还引出了一个思考：

如果使用三分法、四分法等策略进行排序，是否能进一步提高效率？

答案就体现在线性排序算法中，如 IBM Sort 所采用的——基数排序，它就像是一个多分法游戏。

基数排序之所以效率高，是因为它打破了传统的二分法比较排序算法，采用了多分法，自然地超越了 O(NlogN) 的复杂度上限。

但它也有局限，比如适用于整数和字符串排序，对浮点数和复数排序则可能不那么合适。

通过回归排序的本质，我们不仅理解了比较排序的上限，还拓宽了视野，认识到除了传统比较外，还有其他高效的排序方法。

07

工程学的实用与创新

经过对排序算法历史的回顾，我们还停留在理论知识的学习上，但算法书籍中通常在此就告一段落了。

我们的学习应该不止这些，我们至少能学会应用。但现在我们连自己调用的 sort 方法使用的是什么排序都不知道。

在追求极致效率的今天，现代排序算法已经根据数据量的不同采用不同的排序策略，这种多样化的排序方法被统称为复合型排序算法。

在多数现代编程库中，广泛采用的就是 TimSort 算法——一种融合了插入排序和归并排序优点的复合型排序算法。

这个算法不仅体现了在实用主义基础上的创新，还展示了工程学中对效率和实用性的不懈追求。

因此，文章的结尾并不是结束，而是一个新的开始。通过了解 TimSort 这样站在巨人肩膀上的算法，我们可以开启对算法深层次理解和应用之旅。

好了，这就是我花了 42 天，走完的算法学习从放弃到入门的第一步。

希望通过这篇文章，能够鼓励你真正地踏入算法的世界，理解算法背后的原理，应用在实际问题解决中，乃至于在此基础上进行创新和发展。