1. 图像噪声
图像降噪(Image Denoising)是指从图像中去除 噪声 的过程,目的是提高图像质量,增强图像的视觉效果。
图像噪声是指图像中不希望出现的随机亮度或颜色变化,通常会降低图像的清晰度和可辨识度,以及会降低图像的质量并使图像分析和理解更加困难。
图像噪声主要有以下几个原因来产生的:
光线不足 :光线不足会导致光子噪声增加,从而降低图像的信噪比。
电子元器件的热噪声 :电子元器件在工作时会产生热噪声,这种噪声会影响图像的质量。
电路噪声 :电路中的电磁干扰也会导致图像噪声的产生。
图像传输过程中的错误 :图像在传输过程中可能会受到各种干扰,从而导致图像噪声的产生。
根据噪声的统计特性来分类,可以将图像噪声分为以下几类:
椒盐噪声 :图像中随机出现黑白像素的噪声。
高斯噪声 :最常见的噪声类型,其概率密度函数服从高斯分布。
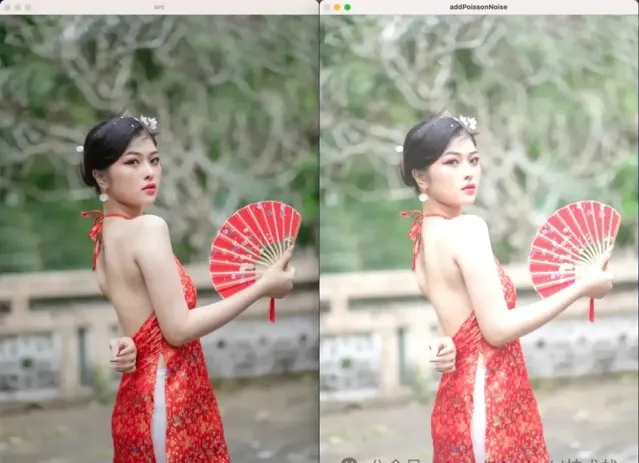
泊松噪声 :光子噪声的一种类型,其概率密度函数服从泊松分布。
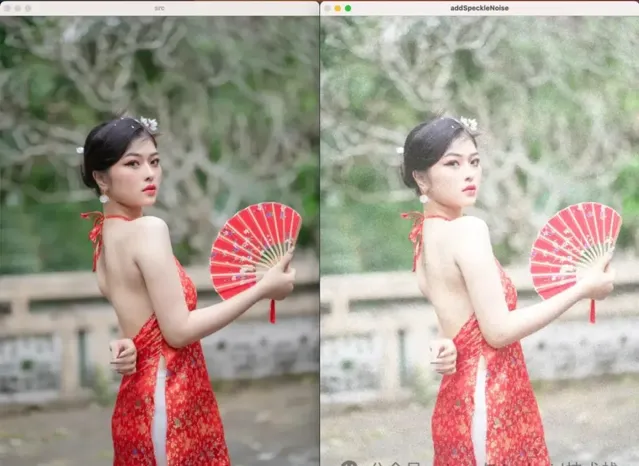
斑点噪声 :由图像传感器坏点或污点引起的噪声。
下面的例子,分别展示了在图像中添加椒盐噪声、高斯噪声、泊松噪声和斑点噪声。
#include<opencv2/opencv.hpp>
#include<opencv2/core.hpp>
#include<opencv2/highgui.hpp>
#include<random>
usingnamespacestd;
usingnamespace cv;
voidaddSaltNoise(Mat &src, int num, Mat &dst)
{
dst = src.clone();
// 随机数产生器
std::random_device rd; //种子
std::mt19937 gen(rd()); // 随机数引擎
auto rows = src.rows; // 行数
auto cols = src.cols * src.channels();
for (int i = 0; i < num; i++)
{
auto row = static_cast<int>(gen() % rows);
auto col = static_cast<int>(gen() % cols);
auto p = dst.ptr<uchar>(row);
p[col++] = 255;
p[col++] = 255;
p[col] = 255;
}
}
voidaddGaussianNoise(Mat &src, int mu, int sigma, Mat &dst)
{
dst = src.clone();
// 产生高斯分布的随机数发生器
std::random_device rd;
std::mt19937 gen(rd());
std::normal_distribution<> d(mu, sigma);
auto rows = src.rows; // 行数
auto cols = src.cols * src.channels(); // 列数
for (int i = 0; i < rows; i++)
{
auto p = dst.ptr<uchar>(i); // 取得行首指针
for (int j = 0; j < cols; j++)
{
auto tmp = p[j] + d(gen);
tmp = tmp > 255 ? 255 : tmp;
tmp = tmp < 0 ? 0 : tmp;
p[j] = tmp;
}
}
}
typedef cv::Point3_<uint8_t> Pixel;
voidaddPoissonNoise(const Mat& src, double lambda, Mat& dst){
dst = src.clone();
// 产生泊松分布的随机数生成器
std::random_device rd;
std::mt19937 gen(rd());
std::poisson_distribution<int> distribution(lambda);
dst.forEach<Pixel>([&](Pixel &p, constint * position) -> void {
int row = position[0];
int col = position[1];
int count = distribution(gen);
dst.at<Vec3b>(row, col) = dst.at<Vec3b>(row, col) + Vec3b(count, count, count);
});
}
voidaddSpeckleNoise(Mat& image, double scale, Mat &dst){
dst = image.clone();
RNG rng;
dst.forEach<Pixel>([&](Pixel &p, constint * position) -> void {
int row = position[0];
int col = position[1];
double random_value = rng.uniform(0.0, 1.0);
double noise_intensity = random_value * scale;
dst.at<Vec3b>(row, col) = dst.at<Vec3b>(row, col) + Vec3b(noise_intensity * 255, noise_intensity * 255, noise_intensity * 255);
});
}
intmain(){
Mat src = imread(".../girl.jpg");
imshow("src", src);
Mat dst1;
addSaltNoise(src,100000,dst1);
imshow("addSaltNoise", dst1);
Mat dst2;
addGaussianNoise(src, 0, 50,dst2);
imshow("addGaussianNoise", dst2);
Mat dst3;
addPoissonNoise(src, 60, dst3);
imshow("addPoissonNoise", dst3);
Mat dst4;
addSpeckleNoise(src,0.5,dst4);
imshow("addSpeckleNoise", dst4);
waitKey(0);
return0;
}

2. 图像降噪方法
传统的图像处理是基于滤波器的方式进行降噪,比如使用空域滤波、频域滤波、非局部均值滤波等等,还有使用形态学降噪,当然也可以深度学习的方式进行降噪。
本文介绍两种空域滤波的方式进行降噪。
2.1 中值滤波
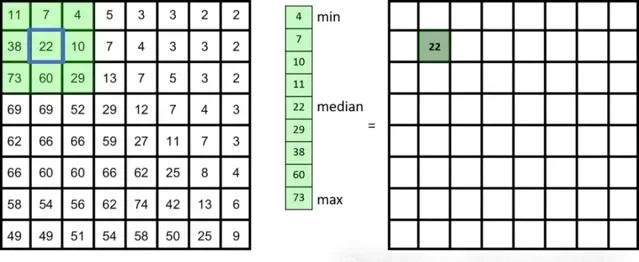
中值滤波是一种 非线性 滤波器,它通过对图像中的像素值进行排序并取中间值来进行滤波处理。
中值滤波的特性:
对于图像中的每个像素,选取其周围一定区域内的所有像素值,并对其进行排序。
将排序后的像素值的中位数赋予该像素。
中值滤波的优点:
能够有效去除椒盐噪声和脉冲噪声,对图像中的孤立噪声点具有较强的抑制能力。
能够较好地保留图像的边缘和细节信息,不会造成图像模糊。
中值滤波的缺点:
对高斯噪声的去除效果不佳。
计算量相对较大,特别是对于大尺寸图像而言。
2.2 高斯滤波
高斯滤波是一种 线性 平滑滤波器,它利用高斯函数对图像进行加权平均,可以有效地去除高斯噪声,同时平滑图像。
高斯滤波的优点:
高斯滤波具有良好的平滑效果,能够有效地抑制图像中的噪声。
高斯滤波是一种线性滤波器,具有可分离性,可以提高计算效率。
高斯滤波在频域上具有低通滤波器的特性,能够去除图像中的高频噪声。
高斯滤波的缺点:
高斯滤波会造成图像细节丢失,降低图像锐度。
高斯滤波对椒盐噪声等非平滑噪声的去除效果不佳。
高斯滤波以使用两种方法实现:一种是离散化窗口滑窗卷积,另一种方法是通过傅里叶变化。最常见的就是滑窗卷积实现。
先来回顾一下一维高斯函数:
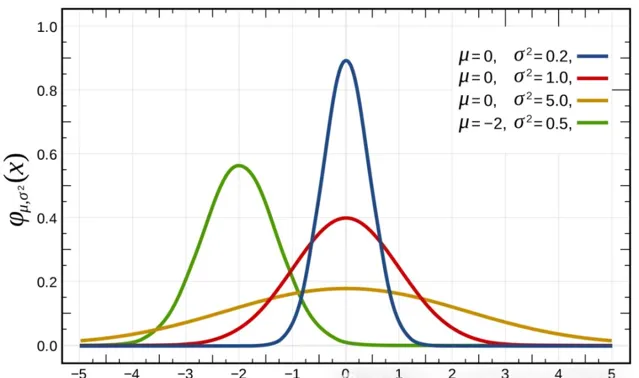
其中,是 x 的均值,是 x 的方差。x 是卷积核内任意一点的坐标,是卷积核中心的坐标。当 = 0 时,
由于图像是二维的,二维的高斯函数则是对 x、y 两个方向的一维高斯函数的乘积:
当时,就是我们比较熟悉的二维高斯函数公式:
常用的高斯模板有如下几种形式,它们是基于高斯函数计算出来的。

高斯滤波具有以下性质:
线性: 高斯滤波器是线性的,这意味着它可以与其他滤波器组合使用。例如,可以先使用高斯滤波器去除噪声,然后再使用边缘检测滤波器检测边缘。
可分离性: 高斯滤波器可以分离为两个一维滤波器,即水平方向和垂直方向的滤波器。这使得高斯滤波器的计算效率更高。
傅里叶变换: 高斯滤波器的傅里叶变换是一个低通滤波器,这意味着它可以抑制图像中的高频成分,而保留低频成分。
旋转不变性: 高斯滤波器在各个方向上具有相同的平滑效果,这意味着它不会改变图像的旋转方向。
尺度不变性: 高斯滤波器的尺度可以通过调整高斯函数的标准差来控制。标准差越大,滤波器的平滑效果越强。
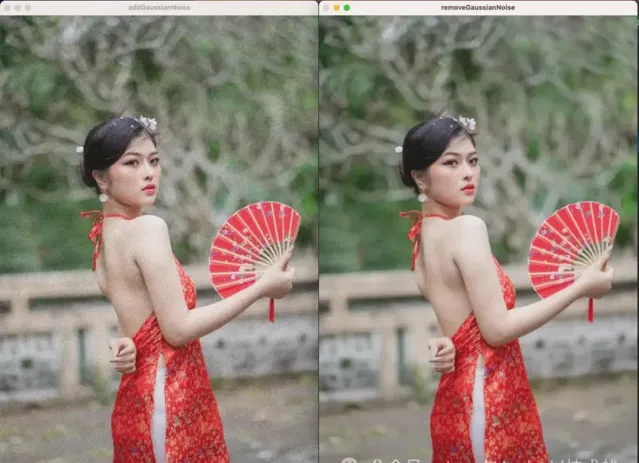
下面的例子,分别使用中值滤波和高斯滤波消除椒盐噪声和高斯噪声。
intmain(){
Mat src = imread(".../girl.jpg");
imshow("src", src);
Mat result;
Mat dst1;
addSaltNoise(src,100000,dst1);
imshow("addSaltNoise", dst1);
int a = 7;
medianBlur(dst1, result,a);
imshow("removeSaltNoise", result);
Mat dst2;
addGaussianNoise(src, 0, 50,dst2);
imshow("addGaussianNoise", dst2);
GaussianBlur(dst2, result, Size(15, 15), 0, 0);
imshow("removeGaussianNoise", result);
waitKey(0);
return0;
}
3. 总结
图像降噪可以提高图像质量、提高图像分析和处理的准确性、提高图像压缩效率以及扩展图像应用范围。
本文介绍了两种简单的降噪算法。中值滤波适用于去除椒盐噪声和脉冲噪声,常用于图像修复和增强。高斯滤波适用于去除高斯噪声、平滑图像,常用于图像预处理和模糊处理。
系统化学习直接扫码查看

推荐阅读












