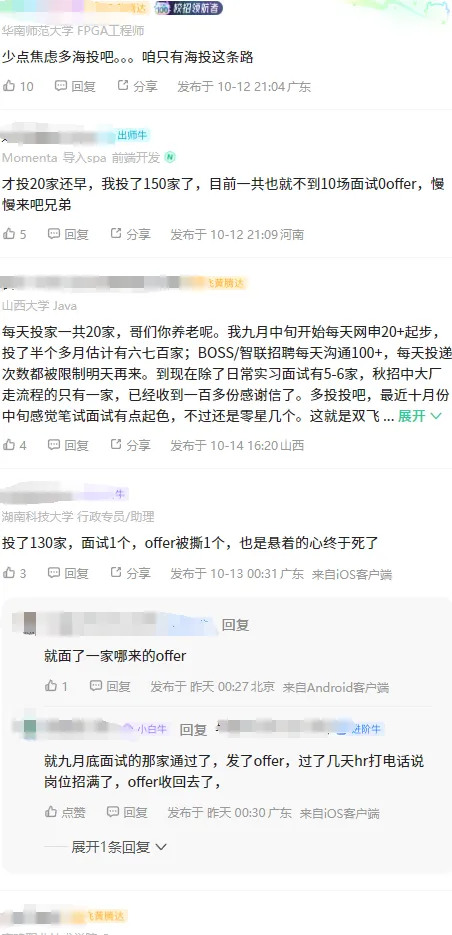
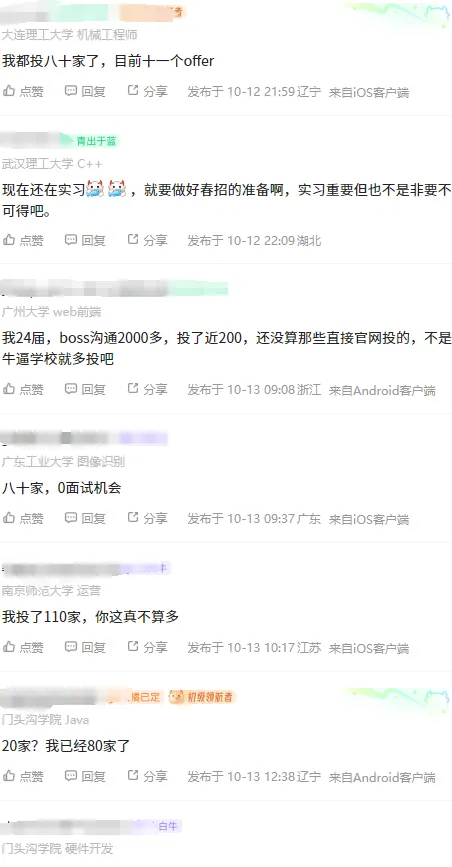
一網友抱怨,每天堅持投5家簡歷,目前已經投了20家,依然是 0 面試。如果是985高校,精準投遞20家也夠了。關鍵安徽工業大學既不是985,也不是211,如果投的都是一些大廠,簡歷被拒的可能性還是存在的, 主要是人太多了, 所以投遞20家明顯不夠,加油繼續投。



--------------下面是今天的演算法題--------------
來看下今天的演算法題,這題是LeetCode的第367題:有效的完全平方數
問題描述
來源:LeetCode第367題
難度:簡單
給你一個正整數 num 。如果 num 是一個完全平方數,則返回 true ,否則返回 false 。不能使用任何內建的庫函式,如 sqrt 。
範例1:
輸入 :num = 16
輸出 :true
解釋 :返回 true ,因為 4 * 4 = 16 且 4 是一個整數。
範例2:
輸入 :num = 14
輸出 :false
解釋 :返回 false ,因為 3.742 * 3.742 = 14 但 3.742 不是一個整數。
1 <= num <= 2^31 - 1
問題分析
這題說的是判斷一個數是否是完全平方數,並且不能使用內建的函式sqrt。我們知道計算一個數的平方根可以使用 ,這個之前講過,就不在重復介紹。
我們來看另一種解決方式,根據下面的公式。
(n+1)^2=n^2+2n+1
我們可以得出任何完全平方數都可以表示成: 1+3+ 5 + 7 +……,所以對於一個數 我們從 1 開始減, 然後是 3 , 接著是 5…… ,如果最後等於 0 , 說明它是完全平方數 。
JAVA:
// 任何數的平方都可以寫成 1+3+5+7+...
publicbooleanisPerfectSquare(int num){
int i = 1;
while (num > 0) {
num -= i;
i += 2;
}
return num == 0;
}
C++:
public:
boolisPerfectSquare(int num){
int i = 1;
while (num > 0) {
num -= i;
i += 2;
}
return num == 0;
}
Python:
# 任何數的平方都可以寫成 1+3+5+7+...
defisPerfectSquare(self, num: int) -> bool:
i = 1
while num > 0:
num -= i
i += 2
return num == 0










