如果你想給家添個電視，你的預算會是多少？一千？三千？還是五千？

我閑來無事，就隨手在某個購物軟體上搜了一下「電視機」，就連最廉價的貨色也得千元起步。

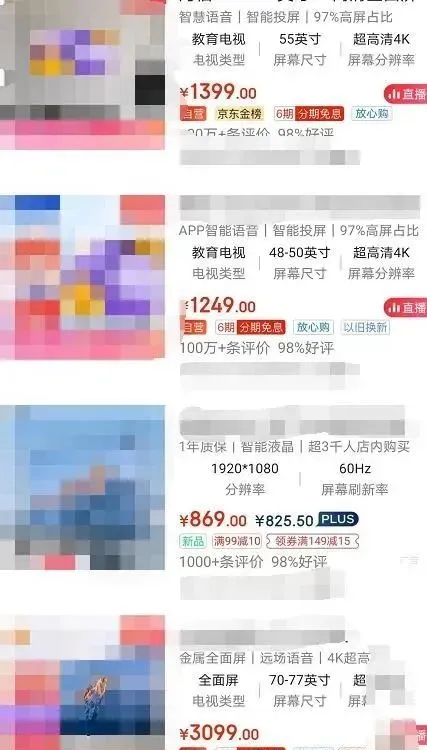
但真的有人會買那些太便宜的電視嗎？難道他們不擔心品質問題，連牌子沒人聽說過，怎麽都感覺不靠譜吧？但是就是這些便宜貨，動不動就是10萬+的銷量。

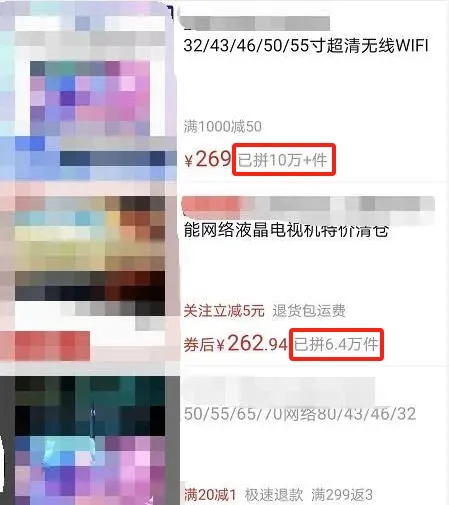
按現在的消費觀來看，200塊錢，可能就是十杯奶茶的價錢，甚至連一頓好的都吃不上。但這麽點錢，竟然能買到一台電視。

翻了翻賣家的圖片，200塊的電視長這樣。

那麽誰會花200塊買這種電視？於是我一翻買家秀，竟一時淚目~

買家曬出的照片裏，這台200塊的電視，有的掛在斑駁的墻上，有的放在亂糟糟的桌子上，旁邊是堆滿了各種雜物的櫃子，有的墻上還掛著孩子的獎狀。一看就知道，這些家庭，生活並不寬裕。

在網上看慣了那些高大上的生活方式，我感覺是我飄了，一開始我竟覺得為什麽會有人買200塊的電視。但實際上，住在出租屋，自己下廚省錢，才是我們的日常。

我們都是普通人，過著普普通通的生活，這就是真相。

下面是今日演算法題

今日演算法題，來自LeetCode的第18題：四數之和，下面是我的演算法思路及實作，讓我們來看看吧。

# 演算法題目

給定一個包含 n 個整數的陣列 nums 和一個目標值 target，找出 nums 中的所有唯一四元組，這四元組的和為 target。每個四元組中的元素必須是不同的。

# 演算法思路

1. 排序：首先對陣列進行排序，這是使用雙指標技術的前提。

   
   

2. 遍歷：使用兩層迴圈遍歷陣列，分別確定前兩個數。對於陣列中的每對數，使用雙指標在剩余部份尋找兩個數，使得這四個數的和等於 target。

   
   

3. 雙指標：在確定了前兩個數後，對陣列的剩余部份使用頭尾雙指標，尋找滿足條件的兩個數。如果找到了，將它們加入到結果列表中。

   
   

4. 去重：在遍歷和雙指標搜尋過程中，需要跳過重復的元素，以確保結果的唯一性。

# 程式碼實作

C語言實作

#include<stdio.h>#include<stdlib.h>// 比較函式，用於 qsortintcompare(constvoid *a, constvoid *b){return (*(int *)a - *(int *)b);}// 主函式int** fourSum(int* nums, int numsSize, int target, int* returnSize, int** returnColumnSizes){ qsort(nums, numsSize, sizeof(int), compare); // 排序int **res = (int **)malloc(sizeof(int *) * 500); // 假設最多有500組解 *returnColumnSizes = (int *)malloc(sizeof(int) * 500); *returnSize = 0;for (int i = 0; i < numsSize - 3; i++) { // 第一個數if (i > 0 && nums[i] == nums[i-1]) continue; // 去重for (int j = i + 1; j < numsSize - 2; j++) { // 第二個數if (j > i + 1 && nums[j] == nums[j-1]) continue; // 去重int left = j + 1, right = numsSize - 1;while (left < right) { // 雙指標尋找int sum = nums[i] + nums[j] + nums[left] + nums[right];if (sum == target) { res[*returnSize] = (int *)malloc(sizeof(int) * 4); res[*returnSize][0] = nums[i]; res[*returnSize][1] = nums[j]; res[*returnSize][2] = nums[left]; res[*returnSize][3] = nums[right]; (*returnColumnSizes)[*returnSize] = 4; (*returnSize)++;while (left < right && nums[left] == nums[left+1]) left++; // 去重while (left < right && nums[right] == nums[right-1]) right--; // 去重 left++; right--; } elseif (sum < target) { left++; } else { right--; } } } }return res;} ‍

Java實作

import java.util.ArrayList;import java.util.Arrays;import java.util.List;public classSolution{publicList<List<Integer>> fourSum(int[] nums, int target) {Arrays.sort(nums);List<List<Integer>> res = new ArrayList<>();for (int i = 0; i < nums.length - 3; i++) {if (i > 0 && nums[i] == nums[i-1]) continue; // 去重for (int j = i + 1; j < nums.length - 2; j++) {if (j > i + 1 && nums[j] == nums[j-1]) continue; // 去重 int left = j + 1, right = nums.length - 1;while (left < right) { int sum = nums[i] + nums[j] + nums[left] + nums[right];if (sum == target) { res.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));while (left < right && nums[left] == nums[left+1]) left++; // 去重while (left < right && nums[right] == nums[right-1]) right--; // 去重left++; right--; } elseif (sum < target) {left++; } else {right--; } } } }return res; }}

Python實作

def four_sum(nums, target): nums.sort() res = []for i in range(len(nums) - 3):if i > 0 and nums[i] == nums[i-1]:continuefor j in range(i + 1, len(nums) - 2):if j > i + 1 and nums[j] == nums[j-1]:continueleft, right = j + 1, len(nums) - 1whileleft < right: sum = nums[i] + nums[j] + nums[left] + nums[right]if sum == target: res.append([nums[i], nums[j], nums[left], nums[right]])whileleft < right and nums[left] == nums[left+1]:left += 1whileleft < right and nums[right] == nums[right-1]:right -= 1left += 1right -= 1 elif sum < target:left += 1else:right -= 1return res ‍

# 演算法解析

這個問題的解法主要依賴於排序和雙指標技術。透過排序，我們可以有效地避免重復解，並且可以使用雙指標技術來降低時間復雜度。整體演算法的時間復雜度為O(n3)，其中 n 是陣列的長度。

# 範例和測試

以輸入陣列 nums = [1, 0, -1, 0, -2, 2] 和目標值 target = 0 為例：

nums = [1, 0, -1, 0, -2, 2]target = 0print(four_sum(nums, target))

輸出：

[[-2, -1, 1, 2], [-2, 0, 0, 2], [-1, 0, 0, 1]]

# 總結

四數之和問題是一個經典的陣列和雙指標問題，透過排序和雙指標技術可以高效地找到所有唯一的四元組。這個方法不僅適用於四數之和問題，也可以擴充套件到三數之和等類似問題。

熱門推薦