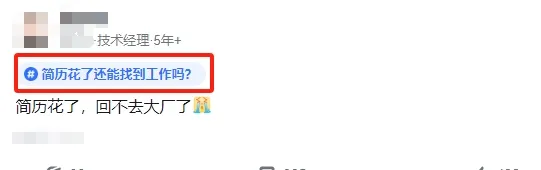
在找工作的時候簡歷就相當於你的門面,那簡歷花了還能找到工作嗎?一網友也是非常困擾:「簡歷花了,回不去大廠了」簡單說一下什麽叫做「簡歷花了」,就是你換工作比較頻繁,缺乏穩定性,所以很多公司看都不看這種簡歷。
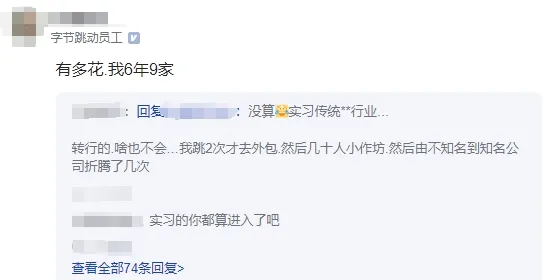
那麽熱心腸的網友是怎麽看待「簡歷花了」呢,有網友就說了:「有多花.我6年9家」不是,哥們,你臨時工啊。
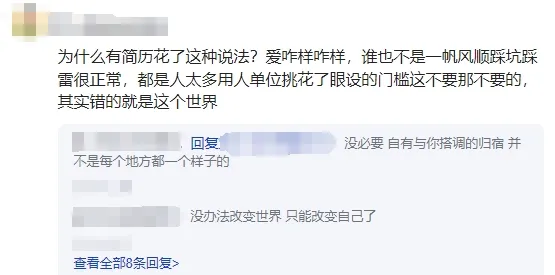
還有網友不屑:「為什麽有簡歷花了這種說法?愛咋樣咋樣,誰也不是一帆風順踩坑踩雷很正常。」說的好,但沒啥用。
更有網友一針見血:「還是因為人太多了慣的」真相了,但大家也無奈啊。
還有網友補傷害:「別慌,到年齡了都差不多。」確實,年齡大了,也是直達垃圾桶。
看完大家的態度,並不是花了,就找不到工作了。但也確確實實有很多公司不會要,所以在你能改變這個世界之前,能不花就不花吧。
那麽問題來了,多久跳一次,才不算花了簡歷呢?參考網友們的意見,至少是2.5年以上,在不影響你規劃的前提下,能待久點就待久點。那麽大家怎麽看呢?
下面是今日的大廠演算法題
現在環境就這樣,不管是大廠還是小廠,筆面試都會問到演算法,所以演算法無疑是非常重要的。 下面是今日演算法題,來自LeetCode的第47題:全排列 II ,下面是我的演算法思路及實作,讓我們來看看吧。
# 演算法題目
給定一個可能包含重復元素的整數陣列,返回該陣列所有可能的全排列。
# 演算法思路
解決含有重復元素的全排列問題的關鍵是如何避免生成重復的排列。我們可以采用以下步驟:
排序:首先對陣列進行排序,這使得相同的數位都相鄰,便於後續步驟中判斷重復。
遞迴和回溯:使 用遞迴函式生成排列,透過回溯法探索所有可能的排列組合。
使用標記陣列:使用一個標記陣列來記錄哪些數位已經被使用過,從而避免使用相同的數位。
跳過重復的數位:在遞迴的每一層中,如果當前數位與前一個數位相同,並且前一個數位未被使用過,我們應跳過當前數位以避免重復。
# 程式碼實作
Java實作
import java.util.*;public classSolution {public List<List<Integer>> permuteUnique(int[] nums) { Arrays.sort(nums); List<List<Integer>> results = new ArrayList<>(); backtrack(results, new ArrayList<>(), nums, new boolean[nums.length]);return results; }privatevoidbacktrack(List<List<Integer>> results, List<Integer> tempList, int[] nums, boolean[] used) {if (tempList.size() == nums.length) { results.add(new ArrayList<>(tempList)); } else {for (int i = 0; i < nums.length; i++) {if (used[i] || (i > 0 && nums[i] == nums[i-1] && !used[i-1])) continue; tempList.add(nums[i]); used[i] = true; backtrack(results, tempList, nums, used); tempList.remove(tempList.size() - 1); used[i] = false; } } }}
JavaScript實作
functionpermuteUnique(nums) { nums.sort((a, b) => a - b);const results = [];const backtrack = (path, used) => {if (path.length === nums.length) { results.push([...path]);return; }for (let i = 0; i < nums.length; i++) {if (used[i] || (i > 0 && nums[i] === nums[i - 1] && !used[i - 1])) {continue; } path.push(nums[i]); used[i] = true; backtrack(path, used); path.pop(); used[i] = false; } }; backtrack([], Array(nums.length).fill(false));return results;}
Go實作
import"sort"funcpermuteUnique(nums []int) [][]int { sort.Ints(nums)var results [][]intvar backtrack func(path []int, used []bool)backtrack = func(path []int, used []bool) {iflen(path) == len(nums) { result := make([]int, len(path))copy(result, path) results = append(results, result)return }for i := 0; i < len(nums); i++ {if used[i] || (i > 0 && nums[i] == nums[i-1] && !used[i-1]) {continue } used[i] = true path = append(path, nums[i]) backtrack(path, used) path = path[:len(path)-1] used[i] = false } } backtrack([]int{}, make([]bool, len(nums)))return results}
Python 實作
defpermuteUnique(nums):defbacktrack(path, used):if len(path) == len(nums): results.append(path[:])returnfor i in range(len(nums)):if used[i] or (i > 0and nums[i] == nums[i-1] andnot used[i-1]):continue used[i] = true path.append(nums[i]) backtrack(path, used) path.pop() used[i] = false nums.sort() results = [] backtrack([], [False] * len(nums))return results
# 演算法解析
在所有實作中,我們首先對陣列進行排序,以簡化重復元素的檢測。然後,我們透過回溯法探索所有可能的元素組合,同時使用一個布爾陣列來跟蹤哪些元素已經被使用過。
當我們遇到一個已經使用過的元素或者當前元素與前一個元素相同且前一個元素未被使用時,我們跳過當前元素,從而避免產生重復的排列。
# 範例和測試
python
nums = [1, 1, 2]print(permuteUnique(nums)) # 輸出: [[1, 1, 2], [1, 2, 1], [2, 1, 1]]
javascript
console.log(permuteUnique([1, 1, 2])); // 輸出: [[1, 1, 2], [1, 2, 1], [2, 1, 1]]
java
System.out.println(new Solution().permuteUnique(newint[]{1, 1, 2}));// 輸出: [[1, 1, 2], [1, 2, 1], [2, 1, 1]]
go
fmt.Println(permuteUnique([]int{1, 1, 2})) // 輸出: [[1, 1, 2], [1, 2, 1], [2, 1, 1]]
# 總結
透過本文的詳細討論和程式碼範例,我們可以看到,盡管輸入陣列可能包含重復元素,我們仍然能夠有效地生成所有不重復的全排列。

熱門推薦











