網路是由一些緊密相連的節點組成的,並且根據不同節點之間連線的緊密程度,網路也可視為由不同簇組成。簇內的節點之間有著更為緊密的連線,不同簇之間的連線則相對稀疏。這種簇被稱為
網路中的社群結構
(community structure)。
由此衍生出來的 社群發現 (community detection)演算法用來發現網路中的社群結構,這類演算法包括 Louvain 演算法、Girvan-Newman 演算法以及 Bron-Kerbosch 演算法等。
最近,在 GitHub 上發現了一個可以發現圖中社群結構的 Python 庫 communities,該庫由軟體工程師 Jonathan Shobrook 建立。
計畫地址:https://github.com/shobrook/communities
首先,該庫可以實作以下幾種社群發現演算法:
Louvain 演算法
Girvan-Newman 演算法
層次聚類
譜聚類
Bron-Kerbosch 演算法
其次,使用者還可以使用 communities 庫來視覺化上述幾種演算法,下圖為空手道俱樂部(Zachary's karate club)網路中 Louvain 演算法的視覺化結果:
該庫的安裝方法也非常簡單,可采用 pip 的方式安裝 communities,程式碼如下:
import numpy as np
from communities.algorithms import louvain_method
adj_matrix = np.array([[0, 1, 1, 0, 0, 0],
[1, 0, 1, 0, 0, 0],
[1, 1, 0, 1, 0, 0],
[0, 0, 1, 0, 1, 1],
[0, 0, 0, 1, 0, 1],
[0, 0, 0, 1, 1, 0]])
communities, _ = louvain_method(adj_matrix)
>> communities
[{0, 1, 2}, {3, 4, 5}]
對於這個 Python 庫,很多網友給予了高度評價,表示會去嘗試。
演算法詳解
1、Louvain 演算法
louvain_method(adj_matrix : numpy.ndarray, n : int = None) -> list
該演算法來源於文章【Fast unfolding of communities in large networks】,簡稱為 Louvian。
作為一種基於模組度(Modularity)的社群發現演算法,Louvain 演算法在效率和效果上都表現比較好,並且能夠發現層次性的社群結構,其最佳化的目標是最大化整個圖內容結構(社群網路)的模組度。
Louvain 演算法對最大化圖模組性的社群進行貪婪搜尋。如果一個圖具有高密度的群體內邊緣和低密度的群體間邊緣,則稱之為模圖。
範例程式碼如下:
from communities.algorithms import louvain_methodad
j_matrix = [...]
communities, _ = louvain_method(adj_matrix)
2、Girvan-Newman 演算法
girvan_newman(adj_matrix : numpy.ndarray, n : int = None) -> list
該演算法來源於文章【Community structure in social and biological networks】。
Girvan-Newman 演算法叠代刪除邊以建立更多連線的元件。每個元件都被視為一個 community,當模組度不能再增延長,演算法停止去除邊緣。
範例程式碼如下:
from communities.algorithms import girvan_newman
adj_matrix = [...]
communities, _ = girvan_newman(adj_matrix)
3、層次聚類
hierarchical_clustering(adj_matrix : numpy.ndarray, metric : str = "cosine", linkage : str = "single", n : int = None) -> list
層次聚類實作了一種自底向上、分層的聚類演算法。每個節點從自己 的社群開始,然後,隨著階層的建立,最相似的社群被合並。社群會一直被合並,直到在模組度方面沒有進一步的進展。
範例程式碼如下:
from communities.algorithms import hierarchical_clustering
adj_matrix = [...]
communities = hierarchical_clustering(adj_matrix, metric="euclidean", linkage="complete")
4、譜聚類
spectral_clustering(adj_matrix : numpy.ndarray, k : int) -> list
這種型別的演算法假定鄰接矩陣的特征值包含有關社群結構的資訊。
範例程式碼如下:
from communities.algorithms import spectral_clustering
adj_matrix = [...]
communities = spectral_clustering(adj_matrix, k=5)
5、Bron-Kerbosch 演算法
bron_kerbosch(adj_matrix : numpy.ndarray, pivot : bool = False) -> list
Bron-Kerbosch 演算法實作用於最大團檢測(maximal clique detection)。圖中的最大團是形成一個完整圖的節點子集,如果向該子集中添加其他節點,則它將不再完整。將最大團視為社群是合理的,因為團是圖中連線最緊密的節點群。因為一個節點可以是多個社群的成員,所以該演算法有時會辨識重疊的社群。
範例程式碼如下:
from communities.algorithms import bron_kerbosch
adj_matrix = [...]
communities = bron_kerbosch(adj_matrix, pivot=True)
視覺化
繪圖
draw_communities(adj_matrix : numpy.ndarray, communities : list, dark : bool = False, filename : str = None, seed : int = 1)
視覺化圖(graph),將節點分組至它們所屬的社群和顏色編碼中。返回代表繪圖的 matplotlib.axes.Axes。範例程式碼如下:
from communities.algorithms import louvain_method
from communities.visualization import draw_communities
adj_matrix = [...]
communities, frames = louvain_method(adj_matrix)
draw_communities(adj_matrix, communities)
視覺化圖如下:
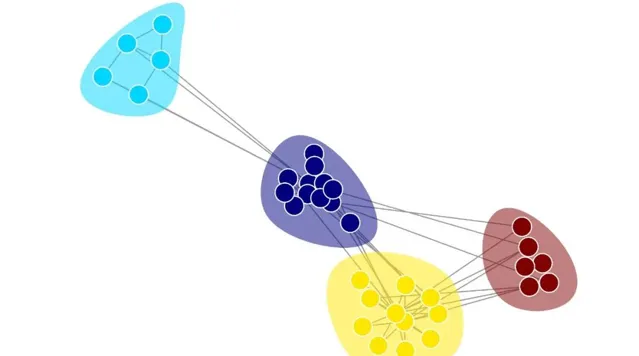
Louvain 演算法的動圖展示
louvain_animation(adj_matrix : numpy.ndarray, frames : list, dark : bool = False, duration : int = 15, filename : str = None, dpi : int = None, seed : int = 2)
Louvain 演算法在圖中的套用可以實作動圖展示,其中每個節點的顏色代表其所屬的社群,並且同一社群中的節點聚類結合在一起。
範例程式碼如下:
from communities.algorithms import louvain_method
from communities.visualization import louvain_animation
adj_matrix = [...]
communities, frames = louvain_method(adj_matrix)
louvain_animation(adj_matrix, frames)
動圖展示如下:
來源:任識演算法
參考連結:
https://www.codenong.com/cs105912940/
https://www.reddit.com/r/MachineLearning/comments/lozys9/p_i_made_communities_a_library_of_clustering/











