強力推薦：演算法學習從放棄到入門的第一步，我花了 42 天終於走完了

你是不是像我一樣，是一名演算法學習困難戶，每一次都滿懷希望地開始，卻又每一次失望地結束。

如果這聽起來很熟悉，那麽這篇文章正是為你而寫。我們將以全新的視角來探究演算法，采用一種更符合我們大腦自然思維方式的學習方法。

我們將追溯排序演算法的源頭，探討它們在當代編程套用中的演變。每一個環節都充滿挑戰和啟發。

讓我們追隨那些偉大的演算法先驅，揭開數據排序的秘密，理解它們的本質，嘗試真正地走入一次演算法學習的大門。

01

演算法學習的困惑

開啟任何一本演算法相關的書籍，我們常常看到它們從排序演算法講起。我一直有這麽一個困惑，不知道你有沒有，就是為什麽要學習排序演算法？

對於程式設計師而言，排序是一個簡單的任務，比如 SQL 中使用「ORDER BY」，或者程式碼中使用「sort()」方法，就可以快速完成排序。

更讓人覺得可氣的是，認真學習一段時間後，我們發現書上學來的排序演算法，效能完全比不上這些簡單的呼叫。

這會讓人很有挫敗感，因為演算法學習逐漸從實用驅動，變成了面試驅動，它成為了檢測你學習和理解能力的工具。

此外，演算法的固有復雜性確實使得其學習成為一項挑戰。當學習變得抽象且缺乏直接的套用價值時，大多數人的學習方法也變成了死記硬背，學完就忘。

一不小心，學習演算法就像學習英語一樣，一次次地翻開書本，一次次地背到「abandon」後就無疾而終了。

有沒有一種可能，學不好演算法的原因不是因為我們自己，而是教科書的教學方式本身就是錯的？

02

學習演算法就是學習歷史

為什麽簡單呼叫一個排序方法，其效能會超過許多教科書上的演算法呢？

答案其實很簡單：這些書中的演算法大多源於上世紀五六十年代，而你所呼叫的，則是經過無數工程師最佳化之後的現代演算法。

電腦發展的時間太短了，讓人很容易忽略它也是有歷史的。

以數學為例，我們可以更容易理解這一點。古希臘哲學家芝諾對無窮悖論的探索，與牛頓和萊布尼茲對無窮問題的處理，顯然是不一樣的。

你也許沒聽說過芝諾這個名字，因為在微積分的教科書中很少提及。然而，在介紹微積分發展歷程的書籍裏，他是絕對不能缺席的。

從問題到答案的過程中，人類對無窮問題的理解是漸進式的。但教科書往往只給我們最終的答案和方法，忽略了其中的思維過程。

演算法書籍也存在這樣的問題。書中對每個演算法的介紹都很詳盡，但它們略過了這些演算法的發展歷史，其誕生和演變的過程，以及可能走過的彎路。

這非常不符合人類大腦學習和記憶的過程。如果我們將這一環節補上，將演算法學習視為一次歷史之旅，會怎樣呢？

重走一遍從無到有的發現歷程，深入理解其中的思考過程，不僅有助於我們掌握演算法的邏輯本質，也有利於理解電腦思維。

03

數據大爆發

在電腦時代到來之前，你有沒有想過數據是如何被排序的？

在古代，縣衙的書記員會手動將公文、稅收等檔進行分類歸檔，通常依據類別和日期排序，以便於將來的檢索。

但是，當數據量增長到超出人力可處理的範圍時，應該如何應對呢？

19 世紀末，隨著美國人口的快速增長，人口普查的數據處理成為了一項巨大的挑戰。

從 1870 年的 5 個調查科目增加到 1880 年的 200 多個，僅完成 1880 年人口普查的工作就耗時長達 8 年，數據量的大霹靂成為了當時急需解決的問題。

當時，數據被記錄在打孔卡片上，每張卡片上的孔洞代表了不同的資訊。

面對成堆的打孔卡片，如何有效進行排序成為了一個問題，比如如何根據年齡對卡片進行排序。

IBM 提供了一種解決方案，即 IBM Sorter 機器，專門用於對打孔卡片進行排序。

IBM Sorter 的工作原理，實際上是基數排序（Radix Sort）的一個物理實作。

機器擁有 13 個口袋，其中 12 個用於分類卡片上對應的十二行的資訊，還有一個口袋用於處理空白、拒絕和錯誤的卡片。

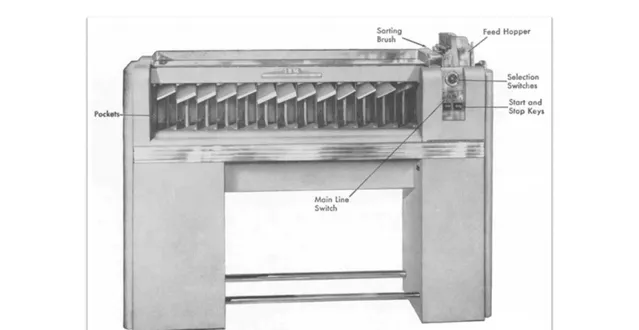
在排序開始前，操作員需要設定好機器，以確定哪一列數據將被用於排序。

例如，如果我們首先根據年齡的個位數排序，機器便會按照這一標準執行，卡片將根據年齡的個位數被分配到不同的口袋中。

隨後，透過對這些個位數已經排序的卡片進行進一步的排序——這次是依據年齡的十位數，我們可以完成全面的排序工作。

進一步地，IBM 還開發了 IBM Collator，這是一種能夠實作兩堆已排序卡片合並的機器。

它的工作原理類似於合並排序演算法，即將兩組已經排序的數據合並成一組有序的數據集。

這些機械式的排序方法，效率遠遠高於當時的人力，它們向我們展示了利用機械化手段處理大規模數據的可能性。

在電腦發明之前，我們已經能夠見證基數排序（Radix Sort）和合並排序在現實世界中的套用。

這不僅是對技術創新的一種展示，也反映了演算法和數據處理技術的發展是一個長期而漸進的過程。

04

拯救電腦的算力

在20世紀40年代，電腦的誕生開啟了數位處理的新時代。

早期的電腦透過數位邏輯電路執行計算任務，如求解微分方程式以計算彈道路徑，顯示了電腦在處理復雜計算方面的巨大潛力。

電腦設計中的邏輯和數學問題引起了馮·諾依曼的興趣。

作為研發小組的顧問，他試圖解決早期電腦設計中的缺陷，並最終提出了儲存程式電腦概念，即著名的馮·諾依曼架構。這一架構為現代電腦的設計奠定了基礎。

為驗證這種設計的實用性，馮·諾依曼選擇排序作為主題，透過比較電腦執行這些演算法的時間與 IBM Collator 這類專用排序機的處理速度來展示電腦的效率。

這也是馮·諾依曼寫的第一個程式，當年是寫在手稿上，高德納發現後將其覆寫為符號化的組合語言。

人們逐漸發現電腦不僅能完成簡單的數據合並任務，還能實作更復雜的完整排序過程。

數據不再儲存在卡片上，而是直接保存在連續的記憶體中，可以透過指標移動來進行排序，從而產生了諸如氣泡排序、選擇排序和插入排序等簡單的排序演算法。

這些基本的排序方法，它們像打麻將時整理牌一樣，在記憶體中重新排列數據。

？

隨著電腦的普及，研究人員發現，大量的電腦算力被用於執行排序操作，估計高達 30% 的算力用於此目的。

這促使了排序演算法進入內卷的時代。

為了最佳化算力的使用，開發者開始探索新的演算法，比如使用遞迴和分治編程技巧的歸並排序。

？

歸並排序演算法雖然有效，但也暴露出對記憶體空間的高需求。

1959年，英國科學家 Tony Hoare 提出了快速排序演算法，它基於相同的遞迴和分治思想，但在記憶體使用上更為高效。

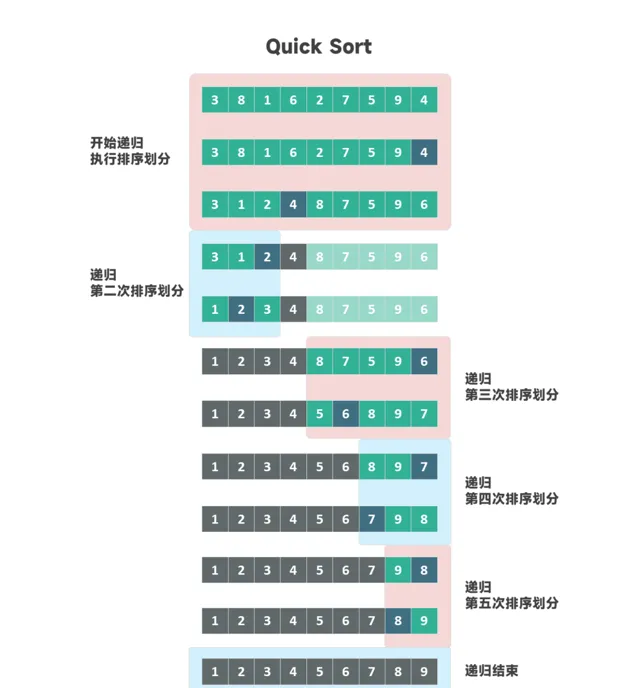
盡管快速排序解決了記憶體使用問題，但它無法保證排序的穩定性——即無法保證相同元素的原始順序。

1964 年加拿大科學家 J.W.J. Williams 發明的堆排序，這種演算法利用堆這一數據結構，提供了又一種排序的解決方案。

這些演算法各有優缺點，哪種演算法更好？評判標準又是什麽？

05

建立評判標準

面對不同場景下演算法效能的評價問題，電腦科學界長期缺乏一個統一的評價標準。

這一問題引發了廣泛的討論，直到 1965 年，Juris Hartmanis 和 Richard Stearns 提出演算法復雜度的概念，為這一討論提供了新的方向。

最終，高德納透過引入 Big O 表示法，提出了一種量化衡量演算法復雜度的方法，他也因此被稱為「演算法分析之父」。

高德納提出的演算法復雜度分析有兩個核心原則：

1. 在評估演算法效率時，應考慮處理極大數據量的場景。之所以關註極大數據量，是因為電腦的設計初衷就是為了處理日益增長的數據量。

2. 雖然影響演算法效能的因素眾多，但它們可大致分為兩類：一類是與數據量無關的固定因素，另一類則是隨數據量增長而變化的因素。在評價演算法優劣時，關鍵在於考察在處理接近無限大的數據集時演算法的表現。

透過這種方法，我們能夠將排序演算法分為兩大類：

時間復雜度為 O(n²) 的演算法，如氣泡排序、選擇排序、插入排序。

時間復雜度為 O(nlog(n)) 的演算法，如歸並排序、快速排序、堆排序。

這一劃分不僅幫助了研究者和開發者在選擇演算法時做出更合理的決策，也促進了電腦科學領域對演算法效能評價標準的統一，推動了電腦演算法的進一步最佳化和發展。

06

回歸排序的本質

在探討排序演算法的發展時，一定會遇到這個問題：是否達到 O(nlog(n)) 的排序演算法就是最優？

要回答這個問題，我們需要從頭開始，重新審視排序的本質。

排序的核心是確定一組元素間的相對順序。對於任意 N 個元素，存在 N! （N 的階乘）種可能的排列，我們的任務是從中找到那唯一滿足排序條件的排列。

排序問題可以被認為是確定元素之間的相對順序。對於任何給定的 N 個元素，都有 N! （N的階乘）種可能的排列，我們的目標是找出那唯一的一種滿足排序需求的排列。

透過比較元素的方式，我們嘗試找到這個「最小」的排列。每次比較實質上是一個二選一的決策，就像猜數位遊戲中的問題，只有「是」或「否」兩種可能。

理想情況下，每次比較都應該將可能性空間平均分割為兩半，這是二分法最優解的基礎，也是比較排序的本質。

從排序演算法的本質出發，我們得出結論：比較排序的理論上限是 O(nlogn) 。

究竟哪種排序演算法最接近這一理論上限呢？答案是那些每次比較都能盡可能將結果分為兩等份的演算法。

透過比較我們可以看到最佳化過的快速堆排序更接近理論上限。

這種對排序本質的探索不僅涵蓋了二分法與排序效率的關系，還引出了一個思考：

如果使用三分法、四分法等策略進行排序，是否能進一步提高效率？

答案就體現線上性排序演算法中，如 IBM Sort 所采用的——基數排序，它就像是一個多分法遊戲。

基數排序之所以效率高，是因為它打破了傳統的二分法比較排序演算法，采用了多分法，自然地超越了 O(NlogN) 的復雜度上限。

但它也有局限，比如適用於整數和字串排序，對浮點數和復數排序則可能不那麽合適。

透過回歸排序的本質，我們不僅理解了比較排序的上限，還拓寬了視野，認識到除了傳統比較外，還有其他高效的排序方法。

07

工程學的實用與創新

經過對排序演算法歷史的回顧，我們還停留在理論知識的學習上，但演算法書籍中通常在此就告一段落了。

我們的學習應該不止這些，我們至少能學會套用。但現在我們連自己呼叫的 sort 方法使用的是什麽排序都不知道。

在追求極致效率的今天，現代排序演算法已經根據數據量的不同采用不同的排序策略，這種多樣化的排序方法被統稱為復合型排序演算法。

在多數現代編程庫中，廣泛采用的就是 TimSort 演算法——一種融合了插入排序和歸並排序優點的復合型排序演算法。

這個演算法不僅體現了在實用主義基礎上的創新，還展示了工程學中對效率和實用性的不懈追求。

因此，文章的結尾並不是結束，而是一個新的開始。透過了解 TimSort 這樣站在巨人肩膀上的演算法，我們可以開啟對演算法深層次理解和套用之旅。

好了，這就是我花了 42 天，走完的演算法學習從放棄到入門的第一步。

希望透過這篇文章，能夠鼓勵你真正地踏入演算法的世界，理解演算法背後的原理，套用在實際問題解決中，乃至於在此基礎上進行創新和發展。