時間序列
在生產和科學研究中,對某一個或者一組變量進行觀察測量,將在一系列時刻所得到的離散數位組成的序列集合,稱之為時間序列。
本文我們就來詳細講講如何用Python進行時間序列分析和預測。主要包括以下內容:
pandas生成時間序列
過濾數據
重采樣
插值
滑窗
數據平穩性與差分法
pandas生成時間序列
時間戳(timestamp)
固定周期(period)
時間間隔(interval)
import pandas as pd
import numpy as np
# TIMES的幾種書寫方式 #2016 Jul 1; 7/1/2016; 1/7/2016 ;2016-07-01; 2016/07/01
rng = pd.date_range('2016-07-01', periods = 10, freq = '3D')#不傳freq則預設是D
rng
DatetimeIndex(['2016-07-01', '2016-07-04', '2016-07-07', '2016-07-10',
'2016-07-13', '2016-07-16', '2016-07-19', '2016-07-22',
'2016-07-25', '2016-07-28'],
dtype='datetime64[ns]', freq='3D')
time=pd.Series(np.random.randn(20),index=pd.date_range('2016-01-01',periods=20))
print(time)
2016-01-01 -1.503070
2016-01-02 1.637771
2016-01-03 -1.527274
2016-01-04 1.202349
2016-01-05 -1.214471
2016-01-06 2.686539
2016-01-07 -0.665813
2016-01-08 1.210834
2016-01-09 0.973659
2016-01-10 -1.003532
2016-01-11 -0.138483
2016-01-12 0.718561
2016-01-13 1.380494
2016-01-14 0.368590
2016-01-15 -0.235975
2016-01-16 -0.847375
2016-01-17 -1.777034
2016-01-18 1.976097
2016-01-19 -0.631212
2016-01-20 -0.613633
Freq: D, dtype: float64
truncate過濾
time.truncate(before='2016-1-10')#1月10之前的都被過濾掉了
time.truncate(after='2016-1-10')#1月10之前的都被過濾掉了
2016-01-01 -1.503070
2016-01-02 1.637771
2016-01-03 -1.527274
2016-01-04 1.202349
2016-01-05 -1.214471
2016-01-06 2.686539
2016-01-07 -0.665813
2016-01-08 1.210834
2016-01-09 0.973659
2016-01-10 -1.003532
Freq: D, dtype: float64
數據重采樣
時間數據由一個頻率轉換到另一個頻率
降采樣
升采樣
import pandas as pd
import numpy as np
rng = pd.date_range('1/1/2011', periods=90, freq='D')#數據按天
ts = pd.Series(np.random.randn(len(rng)), index=rng)
ts.resample('M').sum()#數據降采樣,降為月,指標是求和,也可以平均,自己指定
ts.resample('3D').sum()#數據降采樣,降為3天
day3Ts = ts.resample('3D').mean()
day3Ts
print(day3Ts.resample('D').asfreq())#升采樣,要進行插值
插值方法:
ffill 空值取前面的值
bfill 空值取後面的值
interpolate 線性取值
day3Ts.resample('D').ffill(1)
2011-01-01 0.196793
2011-01-02 0.196793
2011-01-03 NaN
2011-01-04 -0.145891
2011-01-05 -0.145891
...
2011-03-25 NaN
2011-03-26 -0.993341
2011-03-27 -0.993341
2011-03-28 NaN
2011-03-29 -0.022786
Freq: D, Length: 88, dtype: float64
day3Ts.resample('D').bfill(1)
2011-01-01 0.196793
2011-01-02 NaN
2011-01-03 -0.145891
2011-01-04 -0.145891
2011-01-05 NaN
...
2011-03-25 -0.993341
2011-03-26 -0.993341
2011-03-27 NaN
2011-03-28 -0.022786
2011-03-29 -0.022786
Freq: D, Length: 88, dtype: float64
day3Ts.resample('D').interpolate('linear')#線性擬合填充
2011-01-01 0.196793
2011-01-02 0.082565
2011-01-03 -0.031663
2011-01-04 -0.145891
2011-01-05 -0.196231
...
2011-03-25 -0.771202
2011-03-26 -0.993341
2011-03-27 -0.669823
2011-03-28 -0.346305
2011-03-29 -0.022786
Freq: D, Length: 88, dtype: float64
Pandas滑動視窗:
滑動視窗就是能夠根據指定的單位長度來框住時間序列,從而計算框內的統計指標。
相當於一個長度指定的滾軸在刻度尺上面滑動,每滑動一個單位即可反饋滾軸內的數據。
滑動視窗可以使數據更加平穩,浮動範圍會比較小,具有代表性,單獨拿出一個數據可能或多或少會離群,有差異或者錯誤,使用滑動視窗會更規範一些。
%matplotlib inline
import matplotlib.pylab
import numpy as np
import pandas as pd
df = pd.Series(np.random.randn(600), index = pd.date_range('7/1/2016', freq = 'D', periods = 600))
df.head()
2016-07-01 0.391383
2016-07-02 1.529039
2016-07-03 -0.807703
2016-07-04 0.770088
2016-07-05 0.476651
Freq: D, dtype: float64
r = df.rolling(window = 10)
#r.max, r.median, r.std, r.skew傾斜度, r.sum, r.var
print(r.mean())
2016-07-01 NaN
2016-07-02 NaN
2016-07-03 NaN
2016-07-04 NaN
2016-07-05 NaN
...
2018-02-16 0.262464
2018-02-17 0.114787
2018-02-18 0.088134
2018-02-19 0.011999
2018-02-20 0.190583
Freq: D, Length: 600, dtype: float64
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=(15, 5))
df[:].plot(>'r--')
df[:].rolling(window=10).mean().plot(>'b')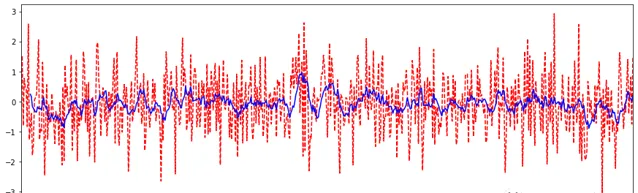
數據平穩性與差分法:
基本模型:自回歸移動平均模型(ARMA(p,q))是時間序列中最為重要的模型之一。
它主要由兩部份組成:AR代表p階自回歸過程,MA代表q階移動平均過程。
平穩性
要求經由時間序列所得到的的擬合曲線在未來一段時間內仍能順著現有形態‘慣性’延續下去
即均值和變異數不發生明顯變化
ARIMA 模型對時間序列的要求是平穩型。
因此,當你得到一個非平穩的時間序列時,首先要做的即是做時間序列的差分,直到得到一個平穩時間序列。
如果你對時間序列做d次差分才能得到一個平穩序列,那麽可以使用ARIMA(p,d,q)模型,其中d是差分次數
ARIMA(p,d,q)
當數據差異特別大時,為了使數據變得平穩些,可以使用差分法
即時間序列在t與t-1時刻的差值
二階差分是指在一階差分基礎上再做一階差分。
%matplotlib inline
import matplotlib.pylab
import numpy as np
import pandas as pd
df = pd.Series(np.random.randn(100), index = pd.date_range('7/1/2016', freq = 'D', periods = 100))
df.head()
2016-07-01 -0.451037
2016-07-02 -1.075953
2016-07-03 0.573926
2016-07-04 -1.643342
2016-07-05 -0.716047
Freq: D, dtype: float64
df.shift(-1) -df
2016-07-01 -0.624916
2016-07-02 1.649879
2016-07-03 -2.217268
2016-07-04 0.927295
2016-07-05 0.127485
df.diff(2)
2016-07-01 NaN
2016-07-02 NaN
2016-07-03 1.024963
2016-07-04 -0.567389
2016-07-05 -1.289973
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #中文支持
plt.rcParams['axes.unicode_minus'] = False#正常顯示負號
x = df.index
y = df
plt.figure(figsize=(15,6))
plt.plot(x,y)
plt.title('原數據')
newx = df.index
y = df.diff(1)
plt.figure(figsize=(15,6))
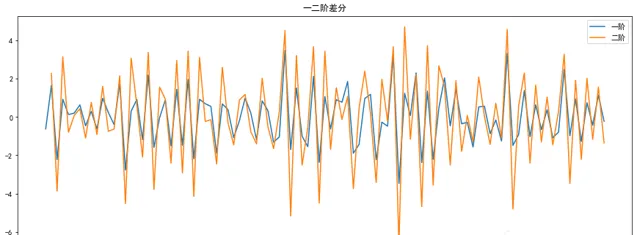
plt.plot(x,y,label = '一階')
plt.title('一二階差分')
y = y.diff(1)
plt.plot(x,y,label = '二階')
plt.legend()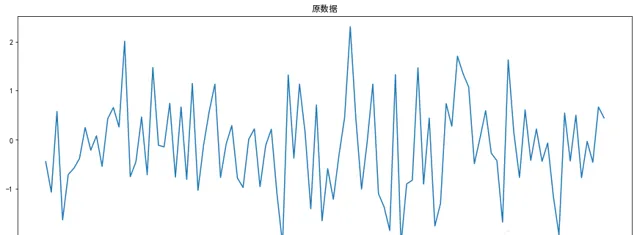
自回歸 AR
用自身變量的歷史時間對自己預測
自回歸模型必須滿足平穩性(可以使用差分)
p階自回歸過程公式: y = u + 求和a*y(t-i) + e
y 是當前值, u是常數項, e 是誤差項(服從獨立同分布) y(t-i)當前預測的值與前P天相關 ,a是自相關系數
自回歸模型限制
用自身來預測
平穩性
自相關性 判斷自相關系數!!
只適用於預測與自身前期相關的現象
移動平均模型(MA)
關註自回歸模型中的誤差項的累加
q階自回歸過程的 定義: y = u + e + b*e(t-i)
移動平均能有效消除預測中的隨機波動
ARIMA
I表示差分項,1是一階,0是不用做,一般做1階就夠了
原理:將非平穩時間序列轉化為平穩時間序列 ,然後將隱變量僅對它的滯後值以及隨機誤差項的現值和滯後值進行回歸所建立的模型。(滯後指階數)
自相關函式ACF
有序的隨機變量與其自身相比較
ACF反映了同一序列在不同時序的取值之間的相關性
ACF(k) = cov(y(t),y(t-k))/var(y(t)) [-1,1]
如何確定 pq參數?
利用ACF 和 PCAF
例項操作
主要分為4部份
用pandas處理時序數據
檢驗序數據的穩定性
處理時序數據變成穩定數據
時序數據的預測
1 用pandas匯入和處理時序數據
數據集是:航空乘客數量預測例子數據集international-airline-passengers.csv
網上一大推:下載地址:https://github.com/sunlei-1997/ML-DL-datasets/blob/master/international-airline-passengers.csv
import numpy as np
import pandas as pd
from datetime import datetime
import matplotlib.pylab as plt
import tqdm
import statsmodels
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima_model import ARIMA
import warnings
warnings.filterwarnings('ignore')
# 讀取數據,pd.read_csv預設生成DataFrame物件,需將其轉換成Series物件
df = pd.read_csv('international-airline-passengers.csv', encoding='utf-8', index_col='Month')
df.index = pd.to_datetime(df.index) # 將字串索引轉換成時間索引
ts = df['Passengers'] # 生成pd.Series物件
ts = ts.astype('float')
ts.head()
Month
1949-01-01 112.0
1949-02-01 118.0
1949-03-01 132.0
1949-04-01 129.0
1949-05-01 121.0
Name: Passengers, dtype: float64
ts.index
DatetimeIndex(['1949-01-01', '1949-02-01', '1949-03-01', '1949-04-01',
'1949-05-01', '1949-06-01', '1949-07-01', '1949-08-01',
'1949-09-01', '1949-10-01',
...
'1960-03-01', '1960-04-01', '1960-05-01', '1960-06-01',
'1960-07-01', '1960-08-01', '1960-09-01', '1960-10-01',
'1960-11-01', '1960-12-01'],
dtype='datetime64[ns]', name='Month', length=144, freq=None)
ts['1949-01-01']
112.0
ts[datetime(1949,1,1)]
112.0
ts['1949-1' : '1949-6']
Month
1949-01-01 112.0
1949-02-01 118.0
1949-03-01 132.0
1949-04-01 129.0
1949-05-01 121.0
1949-06-01 135.0
Name: Passengers, dtype: float64
2 檢驗序數據的穩定性
因為ARIMA模型要求數據是穩定的,所以這一步至關重要。
2.1 判斷數據是穩定的常基於對於時間是常量的幾個統計量:
常量的均值
常量的變異數
與時間獨立的自共變異數
2.2 python判斷時序數據穩定
平穩性檢驗一般采用觀察法和單位根檢驗法。
觀察法:需計算每個時間段內的平均的數據均值和標準差。
單位根檢驗法:透過Dickey-Fuller Test 進行判斷,大致意思就是在一定置信水平下,對於時序數據假設 Null hypothesis: 非穩定。這是一種常用的單位根檢驗方法,它的原假設為序列具有單位根,即非平穩,對於一個平穩的時序數據,就需要在給定的置信水平上顯著,拒絕原假設。
# 移動平均圖
defdraw_trend(timeseries, size):
f = plt.figure(facecolor='white')
# 對size個數據進行移動平均
rol_mean = timeseries.rolling(window=size).mean()
# 對size個數據移動平均的變異數
rol_std = timeseries.rolling(window=size).std()
timeseries.plot(color='blue', label='Original')
rol_mean.plot(color='red', label='Rolling Mean')
rol_std.plot(color='black', label='Rolling standard deviation')
plt.legend(loc='best')
plt.title('Rolling Mean & Standard Deviation')
plt.show()
defdraw_ts(timeseries):
f = plt.figure(facecolor='white')
timeseries.plot(color='blue')
plt.show()
#Dickey-Fuller test:
defteststationarity(ts,max_lag = None):
dftest = statsmodels.tsa.stattools.adfuller(ts,maxlag= max_lag)
# 對上述函式求得的值進行語意描述
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
return dfoutput
#檢視原始數據的均值和變異數
draw_trend(ts,12)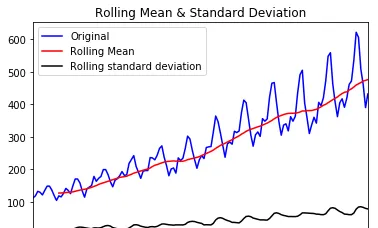
透過上圖,我們可以發現數據的移動平均值/標準差有越來越大的趨勢,是不穩定的。接下來我們再看Dickey-Fuller的結果
teststationarity(ts)
Test Statistic 0.815369
p-value 0.991880
#Lags Used 13.000000
Number of Observations Used 130.000000
Critical Value (1%) -3.481682
Critical Value (5%) -2.884042
Critical Value (10%) -2.578770
dtype: float64
此時p值為0.991880,說明並不能拒絕原假設。透過DF的數據可以明確的看出,在任何置信度下,數據都不是穩定的。
3 處理時序數據變成穩定數據
數據不穩定的原因主要有以下兩點:
趨勢(trend)-數據隨著時間變化。比如說升高或者降低。
季節性(seasonality)-數據在特定的時間段內變動。比如說節假日,或者活動導致數據的異常。
3.1 對數變換
對數變換主要是為了減小數據的振動振幅,使其線性規律更加明顯,同時保留其他資訊。這裏強調一下,變換的序列需要滿足大於0,小於0的數據不存在對數變換。
ts_log = np.log(ts)
draw_trend(ts_log,12)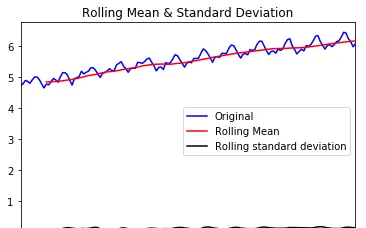
可以看出經過對數變換後,數據值域範圍縮小了,振幅也沒那麽大了。
3.2 平滑法
根據平滑技術的不同,平滑法具體分為移動平均法和指數平均法。
移動平均即利用一定時間間隔內的平均值作為某一期的估計值,而指數平均則是用變權的方法來計算均值。
移動平均:
defdraw_moving(timeSeries, size):
f = plt.figure(facecolor='white')
# 對size個數據進行移動平均
rol_mean = timeSeries.rolling(window=size).mean()
# 對size個數據進行加權移動平均
rol_weighted_mean = pd.Series.ewm(timeSeries, span=size)
rol_weighted_mean=timeSeries.ewm(halflife=size,min_periods=0,adjust=True,ignore_na=False).mean()
timeSeries.plot(color='blue', label='Original')
rol_mean.plot(color='red', label='Rolling Mean')
rol_weighted_mean.plot(color='black', label='Weighted Rolling Mean')
plt.legend(loc='best')
plt.title('Rolling Mean')
plt.show()
draw_moving(ts_log,12)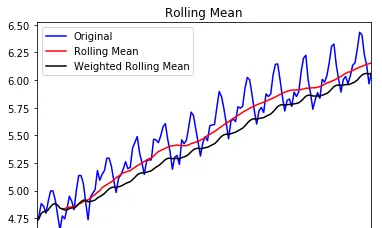
從上圖可以發現視窗為12的移動平均能較好的剔除年周期性因素,
而指數平均法是對周期內的數據進行了加權,能在一定程度上減小年周期因素,但並不能完全剔除,如要完全剔除可以進一步進行差分操作。
3.3 差分
時間序列最常用來剔除周期性因素的方法當屬差分了,它主要是對等周期間隔的數據進行線性求減。
ARIMA模型相對ARMA模型,僅多了差分操作,ARIMA模型幾乎是所有時間序列軟體都支持的,差分的實作與還原都非常方便。
diff_12 = ts_log.diff(12)
diff_12.dropna(inplace=True)
diff_12_1 = diff_12.diff(1)
diff_12_1.dropna(inplace=True)
teststationarity(diff_12_1)
Test Statistic -4.443325
p-value 0.000249
#Lags Used 12.000000
Number of Observations Used 118.000000
Critical Value (1%) -3.487022
Critical Value (5%) -2.886363
Critical Value (10%) -2.580009
dtype: float64
從上面的統計檢驗結果可以看出,經過12階滑動平均和1階差分後,該序列滿足平穩性的要求了。
3.4 分解
所謂分解就是將時序數據分離成不同的成分。
statsmodels使用的X-11分解過程,它主要將時序數據分離成長期趨勢、季節趨勢和隨機成分。
與其它統計軟體一樣,statsmodels也支持兩類分解模型,加法模型和乘法模型,這裏我只實作加法,乘法只需將model的參數設定為"multiplicative"即可。
from statsmodels.tsa.seasonal import seasonal_decompose
defdecompose(timeseries):
# 返回包含三個部份 trend(趨勢部份) , seasonal(季節性部份) 和residual (殘留部份)
decomposition = seasonal_decompose(timeseries)
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid
plt.subplot(411)
plt.plot(ts_log, label='Original')
plt.legend(loc='best')
plt.subplot(412)
plt.plot(trend, label='Trend')
plt.legend(loc='best')
plt.subplot(413)
plt.plot(seasonal,label='Seasonality')
plt.legend(loc='best')
plt.subplot(414)
plt.plot(residual, label='Residuals')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
return trend , seasonal, residual
trend , seasonal, residual = decompose(ts_log)
residual.dropna(inplace=True)
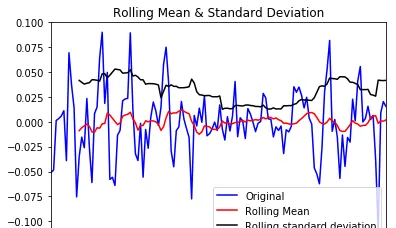
draw_trend(residual,12)
teststationarity(residual)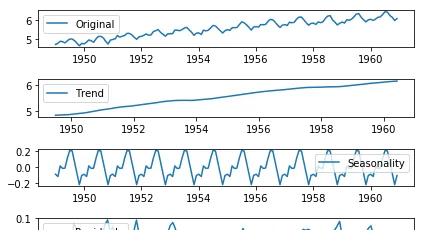
Test Statistic -6.332387e+00
p-value 2.885059e-08
#Lags Used 9.000000e+00
Number of Observations Used 1.220000e+02
Critical Value (1%) -3.485122e+00
Critical Value (5%) -2.885538e+00
Critical Value (10%) -2.579569e+00
dtype: float64
如圖所示,數據的均值和變異數趨於常數,幾乎無波動(看上去比之前的陡峭,但是要註意他的值域只有[-0.05,0.05]之間)
所以直觀上可以認為是穩定的數據。另外DFtest的結果顯示,Statistic值原小於1%時的Critical value,所以在99%的置信度下,數據是穩定的。
4 時序數據的預測
在前面的分析可知,該序列具有明顯的年周期與長期成分。
對於年周期成分我們使用視窗為12的移動平進行處理,對於長期趨勢成分我們采用1階差分來進行處理。
rol_mean = ts_log.rolling(window=12).mean()
rol_mean.dropna(inplace=True)
ts_diff_1 = rol_mean.diff(1)
ts_diff_1.dropna(inplace=True)
teststationarity(ts_diff_1)
Test Statistic -2.709577
p-value 0.072396
#Lags Used 12.000000
Number of Observations Used 119.000000
Critical Value (1%) -3.486535
Critical Value (5%) -2.886151
Critical Value (10%) -2.579896
dtype: float64
觀察其統計量發現該序列在置信水平為95%的區間下並不顯著,我們對其進行再次一階差分。
再次差分後的序列其自相關具有快速衰減的特點,t統計量在99%的置信水平下是顯著的,這裏我不再做詳細說明。
ts_diff_2 = ts_diff_1.diff(1)
ts_diff_2.dropna(inplace=True)
teststationarity(ts_diff_2)
Test Statistic -4.443325
p-value 0.000249
#Lags Used 12.000000
Number of Observations Used 118.000000
Critical Value (1%) -3.487022
Critical Value (5%) -2.886363
Critical Value (10%) -2.580009
dtype: float64
數據平穩後,需要對模型定階,即確定p、q的階數。先畫出ACF,PACF的影像,程式碼如下:
defdraw_acf_pacf(ts,lags):
f = plt.figure(facecolor='white')
ax1 = f.add_subplot(211)
plot_acf(ts,ax=ax1,lags=lags)
ax2 = f.add_subplot(212)
plot_pacf(ts,ax=ax2,lags=lags)
plt.subplots_adjust(hspace=0.5)
plt.show()
draw_acf_pacf(ts_diff_2,30)
觀察上圖,發現自相關和偏相系數都存在拖尾的特點,並且他們都具有明顯的一階相關性,所以我們設定p=1, q=1。
下面就可以使用ARMA模型進行數據擬合了。(Ps.PACF是判定AR模型階數的,也就是p。ACF是判斷MA階數的,也就是q)
model = ARIMA(ts_diff_1, order=(1,1,1))
result_arima = model.fit( disp=-1, method='css')
predict_data=result_arima.predict(15,150) # 擬合+預測0~150數據
forecast=result_arima.forecast(21) # 預測未來21天數據
模型擬合完後,我們就可以對其進行預測了。由於ARMA擬合的是經過相關預處理後的數據,故其預測值需要透過相關逆變換進行還原。
predict_ts = result_arima.predict()
# 一階差分還原
diff_shift_ts = ts_diff_1.shift(1)
diff_recover_1 = predict_ts.add(diff_shift_ts)
# 再次一階差分還原
rol_shift_ts = rol_mean.shift(1)
diff_recover = diff_recover_1.add(rol_shift_ts)
# 移動平均還原
rol_sum = ts_log.rolling(window=11).sum()
rol_recover = diff_recover*12 - rol_sum.shift(1)
# 對數還原
log_recover = np.exp(rol_recover)
log_recover.dropna(inplace=True)
我們使用均方根誤差(RMSE)來評估模型樣本內擬合的好壞。利用該準則進行判別時,需要剔除「非預測」數據的影響。
ts_ = ts[log_recover.index] # 過濾沒有預測的記錄plt.figure(facecolor='white')
log_recover.plot(color='blue', label='Predict')
ts_.plot(color='red', label='Original')
plt.legend(loc='best')
plt.title('RMSE: %.4f'% np.sqrt(sum((log_recover-ts[14:])**2)/ts.size))
plt.show()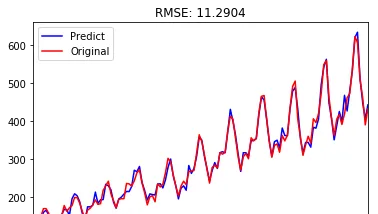
Crossin的新書【 碼上行動:用ChatGPT學會Python編程 】已經上市了。 本書以ChatGPT為輔助,系統全面地講解了如何掌握Python編程,適合Python零基礎入門的讀者學習。
購買後可加入讀者交流群,Crossin為你開啟陪讀模式,解答你在閱讀本書時的一切疑問。
Crossin的其他書籍:
添加微信 crossin123 ,加入編程教室共同學習 ~
感謝 轉發 和 點贊 的各位~











